
| A. | 4 | B. | 0 | C. | 6 | D. | 2 |
分析 原式变形为$\frac{1}{3}$(22-1)(22+1)(24+1)(28+1)…(232+1)+1,反复利用平方差公式计算即可得到结果.
解答 解:(22+1)(24+1)(28+1)…(232+1)+1
=$\frac{1}{3}$×(22-1)(22+1)(24+1)(28+1)…(232+1)+1
=$\frac{1}{3}$×(24-1)(24+1)(28+1)…(232+1)+1
=$\frac{1}{3}$(264-1)+1
=$\frac{{2}^{64}+2}{3}$,
∵21=2,22=4,23=8,24=16,25=32,…,
∴个位上数字以2,4,8,6为循环节循环,
∵64÷4=16,
∴264个位上数字为6,即原式个位上数字为6.
故选C
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.


科目:初中数学 来源: 题型:选择题
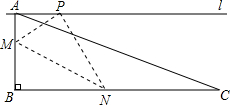 如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )
如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )| A. |  | B. | 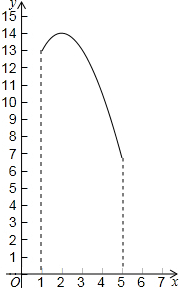 | ||
| C. | 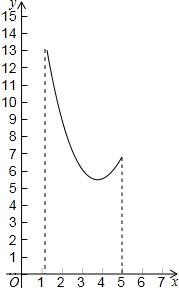 | D. | 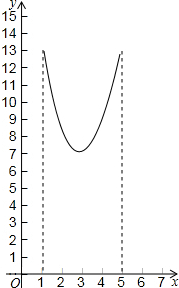 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 9 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
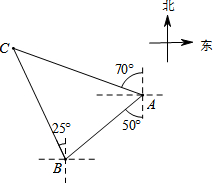 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )| A. | 10$\sqrt{2}$海里 | B. | 10$\sqrt{3}$海里 | C. | 10$\sqrt{6}$海里 | D. | 20$\sqrt{6}$海里 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com