
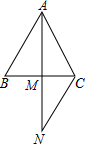
 在△ABC中,AB=AC,过点C作CN∥AB且CN=AC,连接AN交BC于点M.求证:BM=CM.
在△ABC中,AB=AC,过点C作CN∥AB且CN=AC,连接AN交BC于点M.求证:BM=CM.  名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1)2017 | B. | (-3)0 | C. | $\sqrt{9}$ | D. | ($\frac{1}{2}$)-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
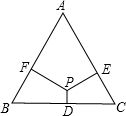 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{20}{3}$ | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≠-2 | B. | a=2 | C. | a=-3 | D. | a=-3或a=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
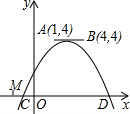 如图,点A,B的坐标分别为(1,4)和(4,4),将抛物线y=a(x-m)2+n平移并保持顶点在线段AB上,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则当点D的横坐标达到最大值时抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4.
如图,点A,B的坐标分别为(1,4)和(4,4),将抛物线y=a(x-m)2+n平移并保持顶点在线段AB上,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则当点D的横坐标达到最大值时抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
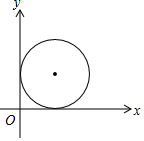 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )| A. | (2018,1) | B. | (4034π+1,1) | C. | (2017,1) | D. | (4034π-1,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com