
【题目】如图,在平面直角坐标系xOy中,AB∥OC,A(0,3),B(a,b),C(c,0),且a,c满足![]() .点P从点A出发,以每秒1个单位长度的速度向点B运动,点Q从点O同时出发,以每秒2个单位长度的速度向点C运动,当点Q到达点C时,点P随之停止运动.设运动时间为t(秒).
.点P从点A出发,以每秒1个单位长度的速度向点B运动,点Q从点O同时出发,以每秒2个单位长度的速度向点C运动,当点Q到达点C时,点P随之停止运动.设运动时间为t(秒).

(1)B,C两点的坐标为:B ,C ;
(2)当t为何值时,四边形PQCB是平行四边形?
(3)D为线段AB的中点,求当t为何值时,△ADQ是等腰三角形?
【答案】(1)![]() ,
,![]() ;(2)当t=4时,四边形PQCB是平行四边形;(3)当t为
;(2)当t=4时,四边形PQCB是平行四边形;(3)当t为![]() ,或
,或![]() ,或2,或
,或2,或![]() 时,△ADQ是等腰三角形.
时,△ADQ是等腰三角形.
【解析】
(1)根据点的坐标特点和二次根式的性质得出a,b,c的值进而得出答案;
(2)由题意得:![]() ,
,![]() ,根据平行四边形的判定可得
,根据平行四边形的判定可得![]() 再解方程即可;
再解方程即可;
(3)分别以AD为腰或AD为底边时情况,根据等腰三角形的性质和勾股定理即可得到结论.
解:(1)∵![]() .
.
∴![]() ,
,
解得a=10,
∴c=14,
∵AB∥OC,A(0,3),
∴b=3,
即B(10,3),C(14,0);
故答案为:(10,3),(14,0)
(2)设运动时间为t(秒),由题意可知:
![]() ,
,![]()
又∵AB∥OC
∴当BP=CQ时,四边形PQCB是平行四边形
此时![]()
解之得![]()
∴当t=4时,四边形PQCB是平行四边形
(3)∵D为线段AB的中点
∴AD=5
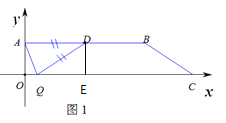
分两种情况:①若AD为腰时,如图1:当DA=DQ=5时,△ADQ是等腰三角形
过点D作DE⊥OC
由题意可知D(5,3)
在Rt△DQE中,![]()
∴OQ=5-4=1,即2t=1
∴![]()
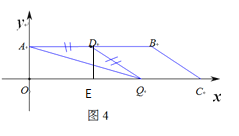
如图3:当AQ=AD=5时,△ADQ是等腰三角形
在Rt△AOQ中,OQ=![]() 4,即2t=4
4,即2t=4
∴![]()
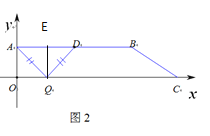
如图4:当DA=DQ时,△ADQ是等腰三角形
过点D作DE⊥OC
在Rt△DQE中,![]()
∴OQ=5+4=9,即2t=9
∴![]()
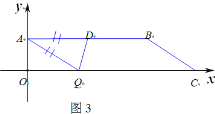
②若AD为底边,如图2:当QA=QD时,△ADQ是等腰三角形
过点Q作QE⊥AB,
∵AB∥OC,∠AOC=90°,QE⊥AB
∴∠∠AOC=∠OQE=∠QEA=90°
∴四边形OQEA是矩形
∴OQ=AE=![]()
即![]() ,
,
∴![]()
综上:当t为![]() 或2或
或2或![]() 或
或![]() 时,△ADQ是等腰三角形
时,△ADQ是等腰三角形


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到![]() 的位置,
的位置,![]() ,
,![]() ,平移距离为6,则阴影部分面积为
,平移距离为6,则阴影部分面积为![]()
![]()

A. 24 B. 40 C. 42 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.

①∵ ∠B=∠3(已知),∴______∥______.(______,______)
②∵∠1=∠D (已知),∴______∥______.(______,______)
③∵∠2=∠A (已知),∴______∥______.(______,______)
④∵∠B+∠BCE=180° (已知),∴______∥______.(______,______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国最长铁路隧道西康铁路秦岭一线隧道全长十八点四六千米,为目前中国铁路隧道长度之首,被称为”神州第一长隧”.为了安全起见在某段隧道两旁安置了两座可旋转探照灯.如图1所示,灯A发出的光束从AC开始顺时针旋转至AD便立即回转,灯B发出的光束从BE开始顺时针旋转至BF便立即回转,两灯不停交叉照射巡视.若灯A旋转的速度是每秒3度,灯B旋转的速度是每秒2度.已知CD∥EF,且∠BAD=![]() ∠BAC,设灯A旋转的时间为t(单位:秒).
∠BAC,设灯A旋转的时间为t(单位:秒).
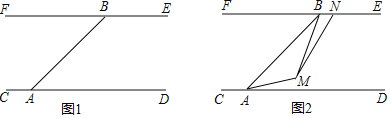
(1)求∠BAD的度数;
(2)若灯B发出的光束先旋转10秒,灯A发出的光束才开始旋转,在灯B发出的光束到达BF之前,若两灯发出的光束互相平行,求灯A旋转的时间t;
(3)如图2,若两灯同时转动,在灯A发出的光束到达AD之前,若两灯发出的光束交于点M,过点M作∠AMN交BE于点N,且∠AMN=135°.请探究:∠BAM与∠BMN的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,连接
上,连接![]() 、
、![]() 交于点
交于点![]() ,且
,且![]() .
.
(1)如图1,求证:![]() .
.

(2)如图2,![]() 是
是![]() 的中点,试探讨
的中点,试探讨![]() 与
与![]() 的位置关系.
的位置关系.

(3)如图3,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,若
的中点,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,直线y=kx+5与x轴交于点A,与抛物线y=ax2+bx交于B,C两点,且点B的坐标为(1,7),点C的横坐标为5.
(1)直接写出k的值和点C的坐标;
(2)将此抛物线沿对称轴向下平移n个单位,当抛物线与直线AB只有一个公共点时,求n的值;
(3)在抛物线上有点P,满足直线AB,AP关于x轴对称,求点P的坐标..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,过
,过![]() 点作与
点作与![]() 垂直的直线
垂直的直线![]() .动点
.动点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动,运动时间为
运动,运动时间为![]() 秒,同时动点
秒,同时动点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 以相同的速度运动,当点
以相同的速度运动,当点![]() 到达点
到达点![]() 时
时![]() 、
、![]() 同时停止运动.
同时停止运动.


(1)请写出![]() 的长为_______,
的长为_______,![]() 的长为_______;
的长为_______;
(2)当![]() 在
在![]() 上
上![]() 在
在![]() 上运动时,如图(2),设
上运动时,如图(2),设![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 为何值时,
为何值时,![]() 为等腰三角形?求出所有满足条件的
为等腰三角形?求出所有满足条件的![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
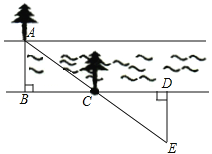
求:(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com