时钟上的分针和时针像两个运动员,绕着它们的跑道昼夜不停地运转.以下请你解答有关时钟的问题:
(1)分针每分钟转了几度?
(2)中午12时整后再经过几分钟,分针与时针所成的钝角会等于121°?
(3)在(2)中所述分针与时针所成的钝角等于121°后,再经过几分钟两针所成的钝角会第二次等于121°?
解:(1)分针每分钟转的度数为360÷60=6(度);
(2)时针每分钟转的度数为360÷(60×12)=0.5(度),设经过x分钟后分针和时针所成的钝角第一次为121度,则(6-0.5)x=121,即5.5x=121,解得x=22(分),
故中午12时整后再经过22分钟,分针与时针所成的钝角会等于121°;
(3)设经过y分钟后分针和时针所成的钝角第二次为121度,两针第二次成121度,也就是360-121=239(度)时,在第一次成121度基础上那就是再经过239-121=118(度),则(6-0.5)y=118,即5.5y=118,解得y=
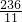
(分)
故分针与时针所成的钝角等于121°后,再经过
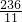
分钟两针所成的钝角会第二次等于121°.
分析:(1)钟表表盘被分成12大格,每一大格又被分为5小格,故表盘共被分成60小格,每一小格所对角的度数为6°.分针每分钟转一个小格,1分钟转动了6度的角;
(2)分针与时针所成的钝角等于121°,可设经过x分钟,然后根据上面的等量关系列方程求解.
(3)两针所成的钝角会第二次等于121°,即360°-121°=239°,然后根据上面的等量关系列方程求解.
点评:本题考查的是钟表表盘与角度相关的特征.钟表表盘被分成12大格,每一大格又被分为5小格,故表盘共被分成60小格,每一小格所对角的度数为6°.分针转动一圈,时间为60分钟,则时针转1大格,即时针转动30°.也就是说,分针转动360°时,时针才转动30°,即分针每转动1°,时针才转动(

)度,逆过来同理.

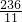 (分)
(分)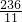 分钟两针所成的钝角会第二次等于121°.
分钟两针所成的钝角会第二次等于121°. )度,逆过来同理.
)度,逆过来同理. 

 名校课堂系列答案
名校课堂系列答案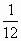 ,即每分钟转了
,即每分钟转了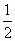 度.你能进一步探索它们的运动规律,提出一些需应用一元一次方程解决的问题吗?
度.你能进一步探索它们的运动规律,提出一些需应用一元一次方程解决的问题吗?