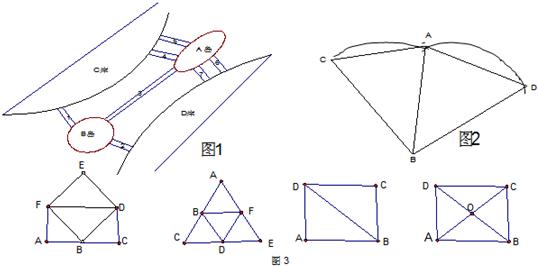
18世纪时，风景秀丽的小城哥尼斯堡中有一条小河，河的中间有两个小岛，河两岸与小岛之间共建有7座桥（图1）．当时小城的居民中流传着一道难题：“一个人怎样走才能不重复地走过所有7座桥，再回到出发点？”
这就是数学史上著名的“7桥问题“，著名的数学家欧拉知道了“7桥问题“，他用四个点A、B、C、D分别表示小岛和河岸，用7条线表示7座桥（图2），于是，问题就成为“如何一笔画出图2中的图形？“欧拉经过研究发现，图2不能一笔画出．这就是说，找不到不重复地经过所有7座桥的路线．
可以想象，凡是“一笔画“，一定有一个“起点“，一个“终点“，还有一些“过路点“，有一条进入过路点，必有一条线离开过路点．这样，与过路点相连的线必为偶数条，而与奇数条线相连的点，只能是起点和终点，这样的点的个数只能是
0或2
0或2
个
如果你还不能填上面的空，请你研究图3的四个图形，根据你的研究结果，把上面的空填上．
在7桥问题中，如果允许你再架一座桥，能否不重复地一次走遍这8座桥？这座桥应建在何处？请你在图2中画出来．并回答有哪几种方式．
