
分析 设他家到学校的路程是xkm,根据每小时骑15km,可早到10分钟,每小时骑12km就会迟到5分钟,列方程即可.
(1)路程,速度,时间的关系是路程=速度×时间;
(2)规定的到校时间是$\frac{x}{15}$+$\frac{10}{60}$或$\frac{x}{12}$-$\frac{5}{60}$.
解答 解:设他家到学校的路程是x km,
由题意得,$\frac{x}{15}$+$\frac{10}{60}$=$\frac{x}{12}$-$\frac{5}{60}$.
故选A.
(1)路程,速度,时间的关系是路程=速度×时间;
(2)规定的到校时间是$\frac{x}{15}$+$\frac{10}{60}$或$\frac{x}{12}$-$\frac{5}{60}$.
故答案为A;路程=速度×时间;$\frac{x}{15}$+$\frac{10}{60}$,$\frac{x}{12}$-$\frac{5}{60}$.
点评 本题考查了一元一次方程的应用,解答本题的关键是读懂题意,找出合适的等量关系,列方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
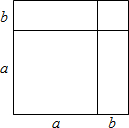 如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )
如图,大正方形的边长为a+b,用两种不同的方法计算这个大正方形的面积,可以推导出的公式是( )| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a-b)2=a2-2ab+b2 | D. | (a+b)2-(a-b)2=4ab |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
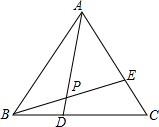 如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )
如图,△ABC是等边三角形,D,E分别在BC和AC上,BD=CE,连接BE交AD于P点,则∠APB的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com