
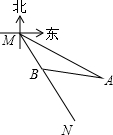
 如图,已知MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区.取MN上另一点B,测得∠ABN=45°.已知MB=400m,如果不改变方向,输水线路是否会穿过居民区?说明理由.
如图,已知MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区.取MN上另一点B,测得∠ABN=45°.已知MB=400m,如果不改变方向,输水线路是否会穿过居民区?说明理由. 分析 问输水线路是否会穿过居民区,其实就是求A到MN的距离是否大于圆形居民区的半径,如果大于则不会穿过,反之则会.
解答 解:不会穿过居民区.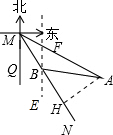
理由是:如图,过A作AH⊥MN于H,作BE∥MQ,交AM于点F.
∵∠EBN=∠QMB=∠FMN=30°,
∴∠NMA=30°,
设AH=x,则BH=x,
∴MH=$\sqrt{3}$AH=$\sqrt{3}$x,
∵MH=BM+BH=x+400,
∴$\sqrt{3}$x=x+400,
∴x=200$\sqrt{3}$+200≈546.4>500
∴不会穿过居民区.
点评 本题考查了解直角三角形,当两个直角三角形有公共的直角边时,利用这条公共边来求解是解决此类题目的基本出发点.


科目:初中数学 来源: 题型:解答题
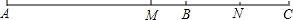 如图,邮递员骑车从邮局B出发,先向南骑行到达M村,继续向南骑行8km到达A村,然后向北骑行到达C村,最后回到邮局B,点M、N分别为AC、BC的中点.
如图,邮递员骑车从邮局B出发,先向南骑行到达M村,继续向南骑行8km到达A村,然后向北骑行到达C村,最后回到邮局B,点M、N分别为AC、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
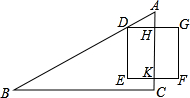 如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,由南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),则城邑的边长为250步.
如图,正方形城邑DEFG的四面正中各有城门,出北门20步的A处(HA=20步)有一树木,由南门14步到C处(KC=14步),再向西行1775步到B处(CB=1775步),正好看到A处的树木(点D在直线AB上),则城邑的边长为250步.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com