
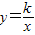 与直线l:y=-kx+b(k>0,b>0)有且只有一个公共点A,AC⊥x轴于C,直线l交x轴于点B.
与直线l:y=-kx+b(k>0,b>0)有且只有一个公共点A,AC⊥x轴于C,直线l交x轴于点B.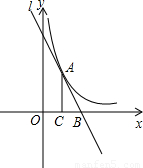
 AC•BC=1可得出k的值,故可得出直线l的方程,列举出动点从原点出发每次向上或向右移动1个单位移动三次时所有可能的结果,再求出该点在直线l上的概率即可.
AC•BC=1可得出k的值,故可得出直线l的方程,列举出动点从原点出发每次向上或向右移动1个单位移动三次时所有可能的结果,再求出该点在直线l上的概率即可. 解:(Ⅰ)联立
解:(Ⅰ)联立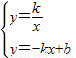 ,得 kx2-bx+k=0.
,得 kx2-bx+k=0. AC•BC=1,即
AC•BC=1,即 •k•1=1,解得:k=2.
•k•1=1,解得:k=2. .
.

科目:初中数学 来源: 题型:解答题
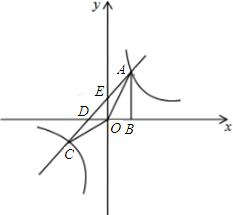 如图,双曲线
如图,双曲线 与直线y=x+(k-1)在第一象限的交点为A,在第三象限的交点为C,过A作AB⊥x轴于点B,且S△ABO=1.5.
与直线y=x+(k-1)在第一象限的交点为A,在第三象限的交点为C,过A作AB⊥x轴于点B,且S△ABO=1.5.查看答案和解析>>
科目:初中数学 来源:2012年河南省信阳市二中中考数学模拟试卷(解析版) 题型:解答题
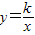 与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3…An的纵坐标是连续整数,分别过A1、A2…An作x轴的平行线于双曲线
与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3…An的纵坐标是连续整数,分别过A1、A2…An作x轴的平行线于双曲线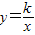 (x>0)及直线x=k分别交于点B1、B2,…Bn,C1、C2,…Cn.
(x>0)及直线x=k分别交于点B1、B2,…Bn,C1、C2,…Cn.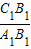 及
及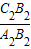 的值;
的值;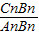 的值(直接写答案).
的值(直接写答案).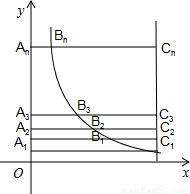
查看答案和解析>>
科目:初中数学 来源:2012年河南省中考数学模拟试卷(七)(解析版) 题型:解答题
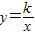 与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3…An的纵坐标是连续整数,分别过A1、A2…An作x轴的平行线于双曲线
与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3…An的纵坐标是连续整数,分别过A1、A2…An作x轴的平行线于双曲线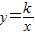 (x>0)及直线x=k分别交于点B1、B2,…Bn,C1、C2,…Cn.
(x>0)及直线x=k分别交于点B1、B2,…Bn,C1、C2,…Cn.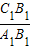 及
及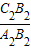 的值;
的值;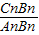 的值(直接写答案).
的值(直接写答案).
查看答案和解析>>
科目:初中数学 来源:2010年辽宁省营口市中考数学试卷(试测)(解析版) 题型:解答题
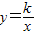 与直线y=ax+b相交于点A(1,5),B(m,-2).
与直线y=ax+b相交于点A(1,5),B(m,-2).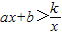 的解集(直接写出答案).
的解集(直接写出答案).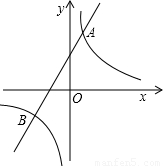
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南信阳市二中中考模拟考试数学试卷(解析版) 题型:解答题
如图,双曲线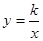 与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3……An的坐标是连续整数,分别过A1、A2……An作x轴的平行线于双曲线
与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3……An的坐标是连续整数,分别过A1、A2……An作x轴的平行线于双曲线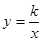 (x>0)及直线x=k分别交于点B1、B2,……Bn,C1、C2,……Cn.
(x>0)及直线x=k分别交于点B1、B2,……Bn,C1、C2,……Cn.
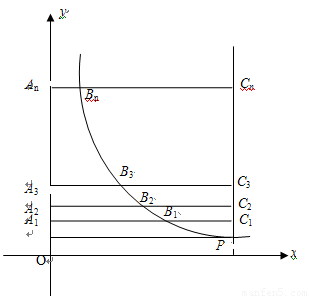
(1)求A的坐标;
(2)求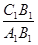 及
及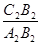 的值;
的值;
(3)猜想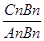 的值(直接写答案).
的值(直接写答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com