
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:选择题
 一个不等式组中两个不等式的解集如图所示,则这个不等式组的解集为( )
一个不等式组中两个不等式的解集如图所示,则这个不等式组的解集为( )| A. | 0≤x≤$\frac{1}{3}$ | B. | x≤$\frac{1}{3}$ | C. | 0≤x<$\frac{1}{3}$ | D. | x>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下
数学课上,王老师在黑板上出示了一道问题让大家回答:题目如下查看答案和解析>>
科目:初中数学 来源: 题型:解答题
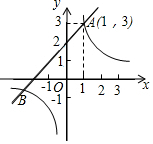 如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3).
如图,已知一次函数y1=x+m的图象与反比例函数y2=$\frac{k}{x}$(k≠0)的图象交于A(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
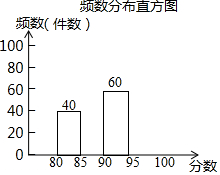 某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:
某县组织了“放飞梦想-我的中国梦”为主题的摄影作品评比活动,全县有1000名学生的作品(每人1件作品)参加了这个评比活动,评比的方法是给每件作品一个分值,最高分100分,最低分80分.现从这1000件作品中随机抽取了m件作品,并把这m件作品的分值制成了如下频数分布表和频数分布直方图:| 分数段 | 频数 | 百分比 |
| 80≤x<85 | 40 | 20% |
| 85≤x<90 | 80 | 40% |
| 90≤x<95 | 60 | 30% |
| 95≤x<100 | 20 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
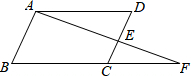 如图,已知:∠DAF=∠F,∠B=∠D,试说明AB∥DC.下面是解答过程,请你在括号内填写理由.
如图,已知:∠DAF=∠F,∠B=∠D,试说明AB∥DC.下面是解答过程,请你在括号内填写理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com