
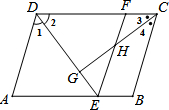
 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可).
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可). 分析 首先根据平行线的性质可得∠1=∠DEF,再根据∠1=∠2,可得∠2=∠DEF,再根据等角对等边可得DF=FE;根据平行四边形的性质可得DF∥AE,再由EF∥AD,可得四边形ADFE是平行四边形,再根据平行四边形的性质可得DF=AE;首先证明∠2+∠3=90°,根据勾股定理可得CG2+DG2=CD2.
解答 解:①∵EF∥AD,
∴∠1=∠DEF,
∵∠1=∠2,
∴∠2=∠DEF,
∴DF=FE,
∵四边形ABCD是平行四边形,
∴DF∥AE,
∵EF∥AD,
∴四边形ADFE是平行四边形,
∴DF=AE;
②∵四边形ABCD是平行四边形,
∴AD∥CB,
∴∠ADC+∠DCB=180°,
∵∠1=∠2,∠3=∠4,
∴∠2+∠3=90°,
∴∠DGC=90°,
∴CG2+DG2=CD2;
故答案为:DF=FE,DF=AE;CG2+DG2=CD2.
点评 此题主要考查了平行四边形的性质,以及勾股定理,关键是掌握平行四边形对边平行且相等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,cosC=$\frac{\sqrt{2}}{2}$,sinB=$\frac{1}{3}$,AD=1.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,cosC=$\frac{\sqrt{2}}{2}$,sinB=$\frac{1}{3}$,AD=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “若x满足(80-x)(x-60)=30,求(80-x)2+(x-60)2的值”
“若x满足(80-x)(x-60)=30,求(80-x)2+(x-60)2的值”查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
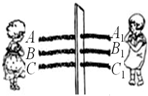 如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.
如图,三根同样的绳子AA1、BB1、CC1穿过一块木板,姐妹两人分别站在木板的左、右两侧,每次各自选取本侧的一根绳子,每根绳子被选中的机会相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com