
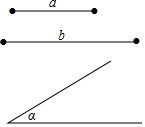
 已知:线段a、b、∠α(如图),用直尺和圆规作一个平行四边形,使它的两条对角线长分别等于线段a、b,且两条对角线所成的一个角等于∠α.
已知:线段a、b、∠α(如图),用直尺和圆规作一个平行四边形,使它的两条对角线长分别等于线段a、b,且两条对角线所成的一个角等于∠α. 分析 先作线段a、b的垂直平分线得到$\frac{1}{2}$a和$\frac{1}{2}$b,再作∠AOB=∠α,且OA=$\frac{1}{2}$a,OB=$\frac{1}{2}$b,然后在OA的反向延长线上截取OD=$\frac{1}{2}$a,在OB的反向延长线上截取OC=$\frac{1}{2}$b,则利用平行四边形的判定方法可判断四边形ABCD为平行四边形.
解答 解:如图,四边形ABCD为所作.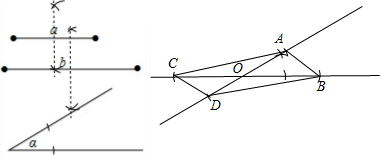
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图是某游乐城的平面示意图,如图用(8,2)表示入口处的位置,用(6,-1)表示球幕电影的位置,那么坐标原点表示的位置是( )
如图是某游乐城的平面示意图,如图用(8,2)表示入口处的位置,用(6,-1)表示球幕电影的位置,那么坐标原点表示的位置是( )| A. | 太空秋千 | B. | 梦幻艺馆 | C. | 海底世界 | D. | 激光战车 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某校教学楼AB的后面有一办公楼CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高3米的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C有30米的距离(B、F、C在一条直线上).现要在A、E之间挂一些彩旗,求A、E之间的距离.(参考数据:sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$,精确到0.1m)
如图,某校教学楼AB的后面有一办公楼CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高3米的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C有30米的距离(B、F、C在一条直线上).现要在A、E之间挂一些彩旗,求A、E之间的距离.(参考数据:sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$,精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
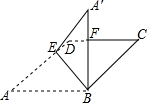 如图,有一张菱形纸片ABCD,∠C=40°,BC=4cm,E为边AD上的点.将△ABE沿BE折叠得到△A′BE,A′B交CD于点F.当A′B⊥CD时,求线段A′F的长.(结果精确到0.1cm)
如图,有一张菱形纸片ABCD,∠C=40°,BC=4cm,E为边AD上的点.将△ABE沿BE折叠得到△A′BE,A′B交CD于点F.当A′B⊥CD时,求线段A′F的长.(结果精确到0.1cm)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲的成绩 | 乙的成绩 | 丙的成绩 | ||||||||||||||
| 环数 | 7 | 8 | 9 | 10 | 环数 | 7 | 8 | 9 | 10 | 环数 | 7 | 8 | 9 | 10 | ||
| 频数 | 1 | 3 | 3 | 1 | 频数 | 2 | 2 | 2 | 2 | 频数 | 3 | 1 | 1 | 3 | ||
| A. | s2甲>s2乙>s2丙 | B. | s2乙>s2甲>s2丙 | C. | s2丙>s2甲>s2乙 | D. | s2丙>s2乙>s2甲 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
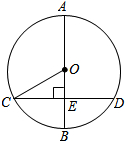 如图,AB是⊙O的直径,弦CD⊥AB于点E,连结CO.如果CO=2cm,∠COE=60°,那么劣弧$\widehat{CD}$的长是$\frac{4}{3}$πcm.
如图,AB是⊙O的直径,弦CD⊥AB于点E,连结CO.如果CO=2cm,∠COE=60°,那么劣弧$\widehat{CD}$的长是$\frac{4}{3}$πcm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com