
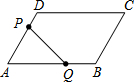
 如图,在平行四边形ABCD中,AB=8cm,AD=4cm,∠A=60°,动点P以2cm/s的速度从D向点A移动,动点Q以4cm/s的速度从点A向点B移动.如果P、Q两点分别从D、A同时出发,当一方到达终点时都随之停止运动,那么经过1秒,五边形PQBCD面积最小.
如图,在平行四边形ABCD中,AB=8cm,AD=4cm,∠A=60°,动点P以2cm/s的速度从D向点A移动,动点Q以4cm/s的速度从点A向点B移动.如果P、Q两点分别从D、A同时出发,当一方到达终点时都随之停止运动,那么经过1秒,五边形PQBCD面积最小. 分析 首先过点P作PH⊥AB于点H,设经过x秒,五边形PQBCD面积最小,则可表示出PD与AQ,又由AB=8cm,AD=4cm,∠A=60°,表示出PH与AP的长,然后由S五边形PQBCD=S?ABCD-S△APQ,可得当△APQ的面积最大时,五边形PQBCD面积最小,继而可得S△APQ=$\frac{1}{2}$AQ•PH=$\frac{1}{2}$×4x×(2$\sqrt{3}$-$\sqrt{3}$x),则可求得答案.
解答  解:过点P作PH⊥AB于点H,设经过x秒,五边形PQBCD面积最小,
解:过点P作PH⊥AB于点H,设经过x秒,五边形PQBCD面积最小,
则PD=2xcm,AQ=4xcm,
∴AP=AD-PD=4-2x(cm),
∵∠A=60°,
∴PH=AP•sin∠A=$\frac{\sqrt{3}}{2}$(4-2x)=2$\sqrt{3}$-$\sqrt{3}$x(cm),
∵S五边形PQBCD=S?ABCD-S△APQ,
∴当△APQ的面积最大时,五边形PQBCD面积最小,
∵S△APQ=$\frac{1}{2}$AQ•PH=$\frac{1}{2}$×4x×(2$\sqrt{3}$-$\sqrt{3}$x)=-2$\sqrt{3}$(x-1)2+2$\sqrt{3}$,
∴当x=1时,五边形PQBCD面积最小.
故答案为:1.
点评 此题考查了平行四边形的性质以及二次函数的最值问题.准确作出辅助线,构造二次函数是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
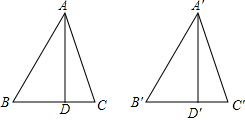 如图,锐角△ABC和锐角△A′B′C′中,AD,A′D′分别是BC,B′C′上的高,且AB=A′B′,AD=A′D′.要使△ABC≌△A′B′C′,则应补充的条件是CD=C′D′(或AC=A′C′,或∠C=∠C′或∠CAD=∠C′A′D′)答案不唯一(填写一个即可).
如图,锐角△ABC和锐角△A′B′C′中,AD,A′D′分别是BC,B′C′上的高,且AB=A′B′,AD=A′D′.要使△ABC≌△A′B′C′,则应补充的条件是CD=C′D′(或AC=A′C′,或∠C=∠C′或∠CAD=∠C′A′D′)答案不唯一(填写一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等腰Rt△ABC中,AB=AC,∠BAC=90°,D为AC上一点,沿BD折叠△ABC,使A点落在BC边上的点E处,M为边BC的中点,MN⊥BD与点H,N在AB边上,连接NE交BD于点G,过点N作BD的平行线交AC于点F,下列结论:①AB=$\sqrt{2}$BN;②四边形DFNG为平行四边形;③△BMN∽△EDG;④AN=DF.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,AB=AC,∠BAC=90°,D为AC上一点,沿BD折叠△ABC,使A点落在BC边上的点E处,M为边BC的中点,MN⊥BD与点H,N在AB边上,连接NE交BD于点G,过点N作BD的平行线交AC于点F,下列结论:①AB=$\sqrt{2}$BN;②四边形DFNG为平行四边形;③△BMN∽△EDG;④AN=DF.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③④ | C. | ①②③ | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com