练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．化简：|x-2|-|x+1|+|x-1|．

    分析 分类讨论x的范围，利用绝对值的代数意义化简，去括号合并即可得到结果．

    解答 解：分四种情况考虑：
    ①当x＜-1时，原式=（2-x）-（-x-1）+（4-x）=7-x；
    ②当-1≤x＜2时，原式=（2-x）-（x+1）+（4-x）=5-3x；
    ③当2≤x＜4时，原式=（x-2）-（x+1）+（4-x）=1-x；
    ④当x≥4时，原式=（x-2）-（x+1）+（x-4）=x-7，
    综上所述：|x-2|-|x+1|+|x-4|=$\left\{\begin{array}{l}{7-x，x＜-1}\\{5-3x，-1≤x＜2}\\{1-x，2≤x＜4}\\{x-7，x≥4}\end{array}\right.$．

    点评 此题考查了整式的加减，以及绝对值，熟练掌握绝对值的代数意义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．已知y+2与2x-3成正比例，且当x=-2时，y=5．
    （1）求y与x的函数关系式；
    （2）当x=2时，求函数y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）若a+b＞0，ab＜0，且|a|=4，|b|=3，求代数式a-b的值．
    （2）若x=2时，代数式a2x3+x2+bx+1的值为3，当x=-2时，求代数式a2x3+x2+bx+1的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知△ABC的两边AB、AC的长分别是关于x的一元二次方程x2-（2k+3）x+k2+3k+2=0的两个实数根，第三边BC的长为5．
    （1）当k为何值时，△ABC是直角三角形；
    （2）当k为何值时，△ABC是等腰三角形，并求出△ABC的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，正方形ABCD内接于⊙O，M为$\widehat{AD}$的中点，连接BM，CM．
    （1）求证：BM=CM；
    （2）求∠BOM的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）已知非零实数a，b满足|a-4|+（b+3）2+$\sqrt{a-4}$+4=a，求a+b的值．
    （2）已知非负实数a，b满足a+b+|$\sqrt{c-1}$-1|=4$\sqrt{a-2}$+2$\sqrt{b+1}$-4，求a+2b-2c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列说法：①121的算术平方根是11；②-$\frac{1}{27}$的立方根是-$\frac{1}{3}$；③-81的平方根是±9；④实数和数轴上的点一一对应，其中错误的有（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

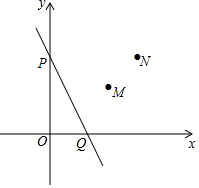    13．如图，直线l：y=-2x+b与两轴交于点P和点Q，点M（3，2），N（4，4）是第一象限内的两点
    （1）当直线l经过M点时，求b的值；
    （2）若点M，N位于l的异侧，确定b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，AB为半圆O的直径，AD、BC分别切⊙O于A，B两点，CD切⊙O于点E，连接OD、OC，下列结论：①∠DOC=90°，②AD+BC=CD，③S△AOD：S△BOC=AD2：AO2，④OD：OC=DE：OE，⑤OD2=DE•CD，正确的有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    同步练习册答案