
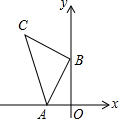
 如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.则点C的坐标是(-n,2+n).(用字母n表示).
如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.则点C的坐标是(-n,2+n).(用字母n表示). 分析 作CE⊥y轴于E,证△CEB≌△BOA,推出CE=OB=n,BE=AO=2,即可得出答案.
解答 解:(1)作CE⊥y轴于E,如图1,
∵A(-2,0),B(0,n),
∴OA=2,OB=n,
∵∠CBA=90°,
∴∠CEB=∠AOB=∠CBA=90°,
∴∠ECB+∠EBC=90°,∠CBE+∠ABO=90°,
∴∠ECB=∠ABO,
在△CBE和△BAO中
$\left\{\begin{array}{l}{∠ECB=∠ABO}\\{∠CEB=∠AOB}\\{BC=AB}\end{array}\right.$,
∴△CBE≌△BAO,
∴CE=BO=n,BE=AO=2,
即OE=2+n,
∴C(-n,2+n).
故答案为:(-n,2+n).
点评 本题考查了全等三角形的性质和判定,三角形内角和定理,等腰三角形性质的应用,主要考查学生综合运用性质进行推理的能力,用了分类讨论思想.


科目:初中数学 来源: 题型:选择题
| A. | 258×107 | B. | 25.8×108 | C. | 2.58×109 | D. | 2.58×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
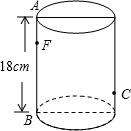 如图,圆柱形无盖玻璃容器,高18cm,底面圆的直径为$\frac{20}{π}$cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.(结果保留根号)
如图,圆柱形无盖玻璃容器,高18cm,底面圆的直径为$\frac{20}{π}$cm,在外侧距下底1cm的点C处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口1cm的F处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com