
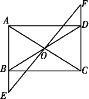
【题目】如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对课本“目标与评定”中的一道思考题,进行了认真的探索。
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
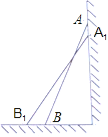
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则B1C=x+0.7,A1C=AC﹣AA1=![]()
而A1B1=2.5,在Rt△A1B1C中,由![]() 得方程 ,
得方程 ,
解方程得x1= ,x2= ,
∴点B将向外移动 米。
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|﹣3|+(﹣1)2016×(π﹣3.14)0﹣(![]() )﹣2+2﹣3
)﹣2+2﹣3
(2)利用乘法公式计算:20182﹣2017×2019
(3)已知2a=3,4b=5,8c=7,求8a+c﹣2b的值.
(4)已知x2﹣5x=14,求(x﹣1)(2x﹣1)﹣(x+1)2+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:① 平方等于64的数是8;② 若a,b互为相反数,ab≠0,则![]() ;③ 若
;③ 若![]() ,则
,则![]() 的值为负数;④ 若ab≠0,则
的值为负数;④ 若ab≠0,则![]() 的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正比例函数y=ax的图象与反比例函数y= ![]() 的图象交于点C(3,1)
的图象交于点C(3,1)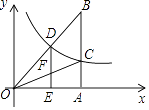
(1)试确定上述比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点D(m,n)是反比例函数图象上的一动点,其中0<m<3,过点C作直线AC⊥x轴于点A,交OD的延长线于点B;若点D是OB的中点,DE⊥x轴于点E,交OC于点F,试求四边形DFCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆检修车沿一段东西方向铁路检修,规定向东走为正,向西走为负,小组的出发地记为M,某天检修完毕时,行走记录(单位:千米)如下:
+12,-5,-9,+10,-4,+15,-9,+3,-6,-3,-7
(1)问收工时,检修小组距出发地M有多远?在东侧还是西侧?
(2)若检修车每千米耗油0.2升,求从出发到收工时检修车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=_____;在图2中,OM是否平分∠CON?请说明理由;
(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com