
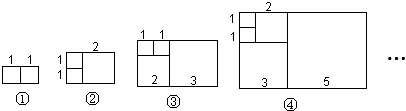
| 序号 | ① | ② | ③ | ④ | … |
| 周长 | 6 | 10 | x | y | … |
分析 结合图形分析表格中图形的周长,①的周长为:2×(1+2),②的周长为:2×(2+3),③的周长为:2×(3+5),④的周长为:2×(5+8),…由此可推出第n个长方形的宽为第n-1个长方形的长,第n个长方形的长为第n-1个长方形的长和宽的和,长方形的周长是前面两个长方形的周长和,由此规律解决问题即可.
解答 解:(1)由分析知:第①个长方形的周长为6=(1+2)×2;
第②个长方形的周长为10=(2+3)×2;
第③个长方形的周长为x=(3+5)×2=16;
第④个长方形的周长为y=(5+8)×2=26;
(2)若按此规律继续拼成长方形,则
第⑤个长方形的周长为42=(8+13)×2;
第⑥个长方形的周长为68=(13+21)×2;
第⑦个长方形的周长为110=(21+34)×2;
第⑧个长方形的周长为178=(34+55)×2;
第⑨个长方形的周长为288=(55+89)×2;
∴序号为⑩的长方形周长是(89+144)×2=466;
故答案为:(1)16,26;(3)466.
点评 此题考查图形的变化规律,要想得到长方形的周长规律,应先找长方形长、宽的变换规律.分析图形中的长和宽,然后结合图表中长方形的周长即可得出长方形周长的变换规律.


科目:初中数学 来源: 题型:选择题
| A. | 0.675×105 | B. | 67.5×103 | C. | 6.75×104 | D. | 6.75×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
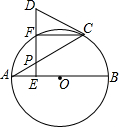 如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,延长EP交$\widehat{AC}$于点F,且在射线EP上找到一点D使得DC=DP.
如图,AB是⊙O的直径,点P是弦AC上一动点(不与A,C重合),过点P作PE⊥AB,垂足为E,延长EP交$\widehat{AC}$于点F,且在射线EP上找到一点D使得DC=DP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| +1 | -1.1 | +2 | +0.7 | -1 | +1.2 | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com