
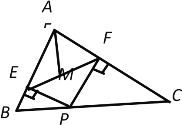
【题目】如图,在△ABC中,AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]() ,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为__________.
,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为__________.
【答案】![]()
【解析】
根据勾股定理的逆定理可以证明∠BAC=90°;根据直角三角形斜边上的中线等于斜边的一半,则AM=![]() EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
EF,要求AM的最小值,即求EF的最小值;根据三个角都是直角的四边形是矩形,得四边形AEPF是矩形,根据矩形的对角线相等,得EF=AP,则EF的最小值即为AP的最小值,根据垂线段最短,知:AP的最小值即等于直角三角形ABC斜边上的高.
∵在△ABC中,AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]()
∴AB2+AC2=18+32=50=BC2
即∠BAC=90°.
又∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=![]() EF=
EF=![]() AP.
AP.
∵AP的最小值为AP⊥BC时,即为直角三角形ABC斜边上的高
∵![]()
∴AP=![]()
∴AM的最小值是![]()
故答案为:![]()


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以水![]() 润
润![]() 城,打造
城,打造![]() 四河一库
四河一库![]() 生态水系工程,是巩义坚持不懈推进文明创建与百城提质深度融合的缩影,伊洛河畔正是此项目中的一段.如今,伊洛河畔需要铺设一条长为
生态水系工程,是巩义坚持不懈推进文明创建与百城提质深度融合的缩影,伊洛河畔正是此项目中的一段.如今,伊洛河畔需要铺设一条长为![]() 米的管道,决定由甲、乙两个工程队来完成.已知甲工程队比乙工程队每天能多铺设
米的管道,决定由甲、乙两个工程队来完成.已知甲工程队比乙工程队每天能多铺设![]() 米,且甲工程队铺设
米,且甲工程队铺设![]() 米所用的天数与乙工程队铺设
米所用的天数与乙工程队铺设![]() 米所用的天数相同.(完成任务的工期为整数)
米所用的天数相同.(完成任务的工期为整数)
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项管道铺设任务的工期不超过![]() 天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为整百数)
天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为整百数)
查看答案和解析>>
科目:初中数学 来源: 题型:
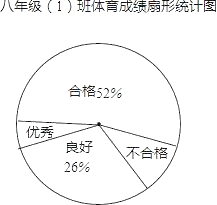
【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
关于x的方程:x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() ;x﹣
;x﹣![]() =c﹣
=c﹣![]() (可变形为x+
(可变形为x+![]() =c+
=c+![]() )的解为x1=c,x2=
)的解为x1=c,x2=![]() ;x+
;x+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Zx+
Zx+![]() =c+
=c+![]() 的解为x1=c,x2=
的解为x1=c,x2=![]() Z.
Z.
(1)归纳结论:根据上述方程与解的特征,得到关于x的方程x+![]() =c+
=c+![]() (m≠0)的解为 .
(m≠0)的解为 .
(2)应用结论:解关于y的方程y﹣a=![]() ﹣
﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
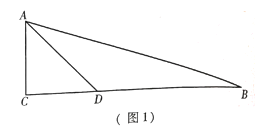
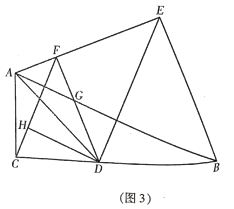
【题目】已知:在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,连结
上,连结![]() ,且
,且![]() .
.
(1)如图1,求![]() 的度数;
的度数;
(2) 如图2, 点![]() 在
在![]() 的垂直平分线上,连接
的垂直平分线上,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求证:
,求证: ![]() 是等腰直角三角形;
是等腰直角三角形;
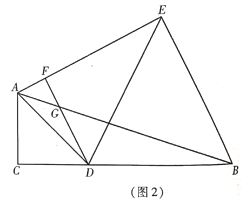
(3)如图3,在(2)的条件下,连接![]() ,过点
,过点![]() 作
作 ![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com