
已知二次函数y=-2x2+4x+6
(1)求函数图象的顶点坐标及对称轴
(2)求此抛物线与x轴的交点坐标.
科目:初中数学 来源:2014-2015学年河北省石家庄市九年级上学期第二次月考数学试卷(解析版) 题型:填空题
两个同心圆的半径分别为3cm和5cm,弦AB与小圆相切于点C,则AB的长为

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,点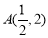 ,
,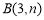 在反比例函数
在反比例函数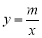 (m为常数)的图象G上,连接AO并延长与图象G的另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象G上,连接AO并延长与图象G的另一个交点为点C,过点A的直线l与x轴的交点为点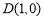 ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
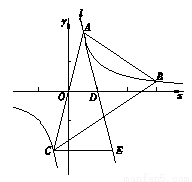
(1)求m的值及直线l对应的函数表达式;
(2)求点E的坐标;
(3)求证:∠BAE=∠ACB.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如果关于x的一元二次方程 有实数根,那么m的取值范围是( )
有实数根,那么m的取值范围是( )
A. B.
B. C.
C. D.
D.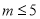
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省心学校九年级上学期数学试卷(解析版) 题型:解答题
已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
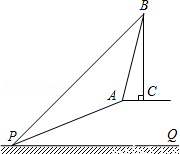
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省心学校九年级上学期数学试卷(解析版) 题型:填空题
如图,A、B两点被池塘隔开,在AB外取一点C,连接AC、BC,在AC上取点M,使AM=3MC,作MN∥AB交BC于N,量得MN=38m,则AB的长为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省心学校九年级上学期数学试卷(解析版) 题型:选择题
若△ABC∽△A′B′C′,其面积比为1:2,则△ABC与△A′B′C′的相似比为( )
A.1:2 B.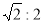 C.1:4 D.
C.1:4 D.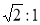
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省七年级上学期期中检测数学试卷(解析版) 题型:填空题
江宁区2010年人口普查结果显示,江宁区常住人口已达115.56万,请你将115.56万用科学记数法表示应是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省自贡市九年级上学期期末统一考试数学试卷(解析版) 题型:解答题
若x1、x2是关于一元二次方程ax2+bx+c(a≠0)的两个根,则方程的两个根x1、x2和系数a、b、c有如下关系:x1+x2=-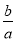 ,x1•x2=
,x1•x2=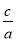 .把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=
.把它称为一元二次方程根与系数关系定理.如果设二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0).利用根与系数关系定理可以得到A、B两个交点间的距离为:AB=|x1-x2|=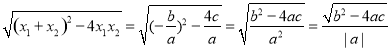 ;
;
参考以上定理和结论,解答下列问题:
设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
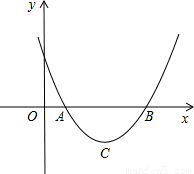
(1)当△ABC为直角三角形时,求b2-4ac的值;
(2)当△ABC为等边三角形时,求b2-4ac的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com