
分析 先算括号里面的,再算除法,减法,最后把x、y的值代入进行计算即可.
解答 解:原式=$\frac{{x}^{2}-xy+xy}{x-y}$•$\frac{(x+y)(x-y)}{{x}^{3}}$-$\frac{1}{x}$
=$\frac{{x}^{2}}{x-y}$•$\frac{(x+y)(x-y)}{{x}^{3}}$-$\frac{1}{x}$
=$\frac{x+y}{x}$-$\frac{1}{x}$
=$\frac{x+y-1}{x}$,
当x=-3,y=2时,原式=$\frac{-3+2-1}{-3}$=$\frac{2}{3}$.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
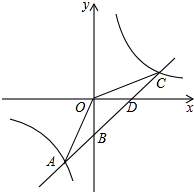 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直角梯形ABCD中,∠A=90°,AD∥BC,AB=AD,DE⊥BC于E,点F为AB上一点,且AF=EC,点M为FC的中点,连结FD、DC、ME,设FC与DE相交于点N,下列结论:
如图,直角梯形ABCD中,∠A=90°,AD∥BC,AB=AD,DE⊥BC于E,点F为AB上一点,且AF=EC,点M为FC的中点,连结FD、DC、ME,设FC与DE相交于点N,下列结论:| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com