
【题目】如图,在四边形ABCD中,BD垂直平分AC,垂足为F,分别过点B作直线BE∥AD,过点A作直线EA⊥AC于点A,两直线交于点E.

(1)求证:四边形AEBD是平行四边形;
(2)如果∠ABE=∠ABD=60°,AD=2,求AC的长.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对任意一个四位数![]() ,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称
,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称![]() 为“极数”;如果一个正整数
为“极数”;如果一个正整数![]() 是另一个正整数
是另一个正整数![]() 的平方,则称正整数
的平方,则称正整数![]() 是完全平方数.若四位数
是完全平方数.若四位数![]() 为“极数”,记
为“极数”,记![]() ,若
,若![]() 是完全平方数,则
是完全平方数,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中小明离家的距离y(km)与时间x(min)之间的对应关系.根据图象,下列说法中正确的是( )
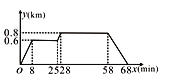
A. 小明吃早餐用了17min
B. 食堂到图书馆的距离为0.8km
C. 小明读报用了28min
D. 小明从图书馆回家的速度为0.8km/min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从![]() 地道
地道![]() 地架设电线,总是尽可能沿着线段
地架设电线,总是尽可能沿着线段![]() 架设;
架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象个数有( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点A,正方形ABCD的顶点B在
轴交于点A,正方形ABCD的顶点B在![]() 轴上,点D在直线
轴上,点D在直线![]() 上,且AO=OB,反比例函数
上,且AO=OB,反比例函数![]() (
(![]() )经过点C.
)经过点C.
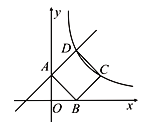
(1)求一次函数和反比例函数的解析式;
(2)点P是![]() 轴上一动点,当
轴上一动点,当![]() 的周长最小时,求出P点的坐标;
的周长最小时,求出P点的坐标;
(3)在(2)的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
(1)当t为何值时,四边形ABQP是矩形;
(2)当t为何值时,四边形AQCP是菱形;
(3)分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店第一次用400元购进胶皮笔记本若干个,第二次又用400元购进该种型号的笔记本,但这次每个的进价是第一次进价的1.25倍,购进数量比第一次少了20个.
(1)求第一次每个笔记本的进价是多少?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后后获利不低于460元,问每个笔记本至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
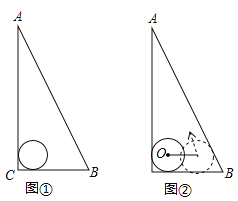
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com