
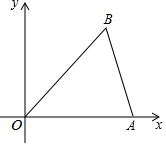
 在平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,3),△AB′O′是△ABO关于点A的位似图形,且点O′的坐标为(-1,0),则点B′的坐标为($\frac{5}{3}$,4).
在平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,3),△AB′O′是△ABO关于点A的位似图形,且点O′的坐标为(-1,0),则点B′的坐标为($\frac{5}{3}$,4). 分析 根据位似图形的性质画出图形,利用对应边之间的关系得出B′点坐标即可.
解答  解:过点B作BE⊥OA与点E,过点B′作B′E′⊥OA于点E′,
解:过点B作BE⊥OA与点E,过点B′作B′E′⊥OA于点E′,
∵△AB′O′是△ABO关于点A的位似图形,
∴△OAB∽△AB′O′,
∴$\frac{AO}{AO′}$=$\frac{BE}{B′E′}$=$\frac{3}{4}$,
解得:B′E′=4,
由题意可得:△OBE∽△O′B′E′,
则$\frac{BE}{B′E′}$=$\frac{OE}{O′E′}$,
故$\frac{2}{O′E′}$=$\frac{3}{4}$,
解得:O′E′=$\frac{8}{3}$,
∴OE′=$\frac{5}{3}$,
∴点B′的坐标为:($\frac{5}{3}$,4).
故答案为:($\frac{5}{3}$,4).
点评 此题主要考查了位似图形的性质以及相似三角形的性质,根据已知得出对应边之间的关系是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
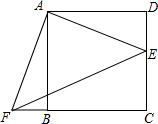 如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在压力不变的情况下,某物体所承受的压强P(pa)与它的受力面积S(m2)之间的函数关系如图所示.
在压力不变的情况下,某物体所承受的压强P(pa)与它的受力面积S(m2)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
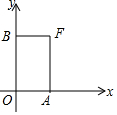 在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAFB的周长与面积相等,则点F是和谐点.
在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图中过点P分别作x轴,y轴的垂线,与坐标轴围成矩形OAFB的周长与面积相等,则点F是和谐点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
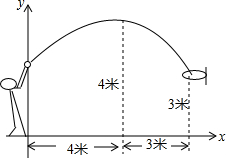 如图示:学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高为$\frac{20}{9}$米,与篮筐中心的水平距离为7米,当球出手后球与队员甲的水平距离为4米时球达到最大高度4米,设篮球运行的轨迹为抛物线,篮筐距地面3米.
如图示:学校九年级的一场篮球比赛中,队员甲正在投篮,已知球出手时离地面高为$\frac{20}{9}$米,与篮筐中心的水平距离为7米,当球出手后球与队员甲的水平距离为4米时球达到最大高度4米,设篮球运行的轨迹为抛物线,篮筐距地面3米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com