
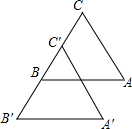
 如图,已知AB∥A′B′,AC∥A′C′且BB′=CC′,求证:△ABC≌△A′B′C′.
如图,已知AB∥A′B′,AC∥A′C′且BB′=CC′,求证:△ABC≌△A′B′C′. 分析 首先根据AB∥A′B′,AC∥A′C′,利用平行线的性质可得:∠ABC=∠B′,∠C=∠A′C′B′,再根据BB′=CC′证出B′C′=BC,可根据三角形全等的判定定理ASA证出△ABC≌△A′B′C′.
解答 证明:∵AB∥A′B′,AC∥A′C′,
∴∠ABC=∠B′,∠C=∠A′C′B′.
∵BB′=CC′,
∴B′C′=BC.
在△ABC和△A′B′C′中
$\left\{\begin{array}{l}{∠ABC=∠B′}\\{BC=B′C′}\\{∠C=∠A′C′B′}\end{array}\right.$,
∴△ABC≌△A′B′C′(ASA).
点评 此题主要考查了全等三角形的判定,关键是熟练掌握判定两个三角形全等的方法:SSS、SAS、ASA、AAS,选用哪一种方法,取决于题目中的已知条件.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | -1 | 0 | 1 |
| ax2 | |||
| ax2+bx+c | 8 | 3 | 0 |
| A. | y=x2-4x+3 | B. | y=x2-2x+4 | C. | y=x2-3x+3 | D. | y=x2-4x+8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
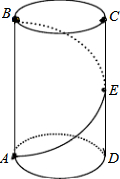 如图,一只螳螂在树干的点A处,发现它的正上方点B处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是就绕到虫子后面吃掉它,已知树干的半径为10cm,A,B两点的距离为45cm,求螳螂爬行的最短距离(π取3).
如图,一只螳螂在树干的点A处,发现它的正上方点B处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是就绕到虫子后面吃掉它,已知树干的半径为10cm,A,B两点的距离为45cm,求螳螂爬行的最短距离(π取3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com