
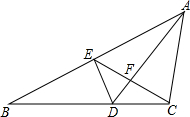
 如图,△ABC中,D为BC上一点,E为AB中点,连接CE、DE,已知AD与EC交于点F,AC=EC,DE⊥AB.
如图,△ABC中,D为BC上一点,E为AB中点,连接CE、DE,已知AD与EC交于点F,AC=EC,DE⊥AB.分析 (1)延长AC,ED交于P,连接PB,由E为AB中点,DE⊥AB,得到AP=PB,由AC=CE,则△PAB和△AEC为等腰三角形,于是得到∠PAB=∠CEA=∠PBA,证得CE∥BP,得到∠PBC=∠BCE,通过△PBD≌△PAD,得到∠CAD=∠PBC,于是得到结论;
(2)延长AD交PB与T,推出△APT≌△BPC,得到PT=PC,证得PT=$\frac{1}{2}$PB,然后通过相似三角形的性质即可得到结论.
解答 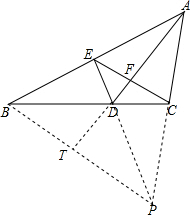 解:(1)延长AC,ED交于P,连接PB,
解:(1)延长AC,ED交于P,连接PB,
∵E为AB中点,DE⊥AB,
∴AP=PB,∵AC=CE,
则△PAB和△AEC为等腰三角形,
∴∠PAB=∠CEA=∠PBA,
∴CE∥BP,
∴∠PBC=∠BCE,
∵AE=EB,ED⊥AB,
∴AD=BD,
在△PBD与△APD中,$\left\{\begin{array}{l}{PA=PB}\\{AD=BD}\\{PD=PD}\end{array}\right.$,
∴△PBD≌△PAD,
∠CAD=∠PBC,
∴∠CAD=∠BCE;
(2)延长AD交PB与T,
在△PAT与△PBC中,$\left\{\begin{array}{l}{∠PBC=∠PAT}\\{PA=PB}\\{∠APT=∠BPC}\end{array}\right.$,
∴△APT≌△BPC,
∴PT=PC,
∵PC=$\frac{1}{2}$PA,
∴PT=$\frac{1}{2}$PB,
∴PT=BT,
∵CE∥BP,
∴△EFD∽△DTP,△CFD∽△DBT,
∴$\frac{EF}{PT}=\frac{FD}{DT}=\frac{FC}{BT}$,
∴EF=CF.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行线的性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
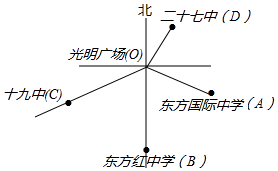 小明在光明广场(点O)绘制了市内几座学校相对广场的位置简图,(图中1cm表示5km),东方红中学在广场正南方向,测得OA=1.7cm,OB=2cm,OC=2cm,OD=1.4cm,∠AOC=123°18′,∠BOA=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?
小明在光明广场(点O)绘制了市内几座学校相对广场的位置简图,(图中1cm表示5km),东方红中学在广场正南方向,测得OA=1.7cm,OB=2cm,OC=2cm,OD=1.4cm,∠AOC=123°18′,∠BOA=68°24′,∠AOD=88°28′,如何确定每个学校的具体位置?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
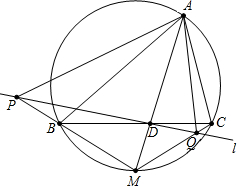 如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )
如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )| A. | 无论直线l的位置如何,总有直线PM与△ABD的外接圆相切 | |
| B. | 无论直线l的位置如何,总有∠PAQ>∠BAC | |
| C. | 直线l选取适当的位置,可使A、P、M、Q四点共圆 | |
| D. | 直线l选取适当的位置,可使S△APQ<S△ABC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
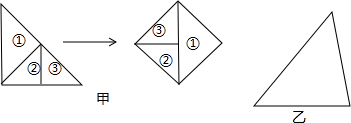
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.71×1013 | B. | 4.72×1013 | C. | 4.71×1012 | D. | 0.472×1014 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
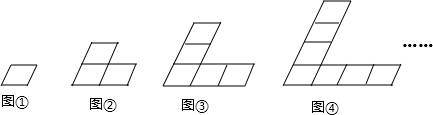
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com