
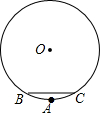
 如图,某健身广场中心修建了一个圆形喷水池,数学活动小组为测量喷水池的半径,选取水池围栏上的A,B,C三根白玉石柱,量得AB=AC,BC长为14m,点A到BC的距离为1m,请你帮他们求出喷水池的半径.
如图,某健身广场中心修建了一个圆形喷水池,数学活动小组为测量喷水池的半径,选取水池围栏上的A,B,C三根白玉石柱,量得AB=AC,BC长为14m,点A到BC的距离为1m,请你帮他们求出喷水池的半径.  夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
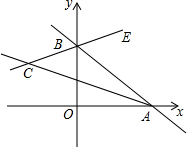 如图,在平面直角坐标系中,已知点A,点B分别是x,y轴的正半轴上的动点,BE是∠ABy的平分线.BE的反向处长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否会发生变化?如果变化,说明你的理由;如果不变,求出∠ACB的度数.
如图,在平面直角坐标系中,已知点A,点B分别是x,y轴的正半轴上的动点,BE是∠ABy的平分线.BE的反向处长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否会发生变化?如果变化,说明你的理由;如果不变,求出∠ACB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com