练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知A=$\root{m-n}{m+n+3}$是m+n+3的算术平方根，B=$\root{m-2n+3}{m+2n}$是m+2n的立方根，求B-A．

    分析 根据算术平方根的定义得出m-n=2，m-n+3=3，求得m，n的值，即可得出答案．

    解答 解：∵A=$\root{m-n}{m+n+3}$是m+n+3的算术平方根，B=$\root{m-2n+3}{m+2n}$是m+2n的立方根，
    ∴$\left\{\begin{array}{l}{m-n=2①}\\{m-2n+3=3②}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{m=4}\\{n=2}\end{array}\right.$，
    ∴A=3，B=2，
    ∴B-A=2-3=-1．

    点评 本题考查了算术平方根和立方根，掌握它们的定义是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

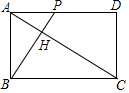    17．如图，已知矩形ABCD中，AB=2，AD=2$\sqrt{3}$，动点P从点A出发向终点D运动，连BP，并过点C作CH⊥BP，垂足为H．①点H不可能在矩形ABCD之外；②AH的最小值为$\sqrt{7}$-$\sqrt{3}$；③在运动过程中，BP扫过的面积始终等于CH扫过的面积；④在运动过程中，点H的运动路线（轨迹）长为$\frac{2}{3}$$\sqrt{3}$π，正确的有（填序号）①②④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．己知A（-1，0），B（2，0），点P是直线y=x+4上的一动点且在x轴上方，如果以点A、B、P、Q为顶点的平行四边形的面积等于6，画出图形并求出点P和点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

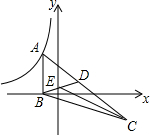    15．如图，△ABC的顶点A在反比例函数y=$\frac{k}{x}$（x＜0）的图象上，AB⊥x轴，垂足为B，顶点C在第四象限，△ABC的中线BD交y轴于点E，连接CE，若△BCE的面积是6，则k的值为-12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．若$\sqrt{x-\frac{1}{8}}$+$\sqrt{\frac{1}{8}-x}$有意义，则$\root{3}{x}$=（　　）
    A．-$\frac{1}{2}$B．$\frac{1}{8}$C．$\frac{1}{2}$D．-$\frac{1}{8}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

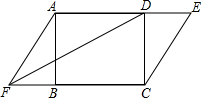    12．如图，在矩形ABCD中，若延长AD至点E，延长CB至点F，并使得DE=BF，连接AF、CE及DF．
    （1）求证：四边形AECF是平行四边形；
    （2）若DE=3，CD=4，AD=5，求证：DF平分∠AFC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，在平面直角坐标系中xOy中，已知点A（0，1），以OA为边在右侧作等边三角形OAA1，再过点A1作x轴的垂线，垂足为点O1，以O1A1为边在右侧作等边三角形O1A1A2；…按此规律继续作下去，得到等边三角形O2016A2016A2017，则点A2017的纵坐标为（　　）
    A．（$\frac{1}{2}$）2017B．（$\frac{1}{2}$）2016C．（$\frac{1}{2}$）2015D．（$\frac{1}{2}$）2014

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

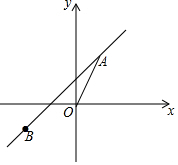    16．如图，正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A（m，2），一次函数的图象经过点B（-2，-1）．
    （1）求一次函数的解析式；
    （2）请直接写出不等式组-1＜kx+b＜2x的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列图标是轴对称图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案