
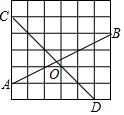
 在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于3.
在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则tan∠BOD的值等于3. 分析 根据平移的性质和锐角三角函数以及勾股定理,通过转化的数学思想可以求得tan∠BOD的值,本题得以解决.
解答 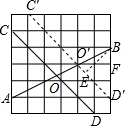 解:平移CD到C′D′交AB于O′,如右图所示,
解:平移CD到C′D′交AB于O′,如右图所示,
则∠BO′D′=∠BOD,
∴tan∠BOD=tan∠BO′D′,
设每个小正方形的边长为a,
则O′B=$\sqrt{{a}^{2}+(2a)^{2}}=\sqrt{5}a$,O′D′=$\sqrt{(2a)^{2}+(2a)^{2}}=2\sqrt{2}a$,BD′=3a,
作BE⊥O′D′于点E,
则BE=$\frac{BD′•O′F}{O′D′}=\frac{3a•2a}{2\sqrt{2}a}=\frac{3\sqrt{2}a}{2}$,
∴O′E=$\sqrt{O′{B}^{2}-B{E}^{2}}=\sqrt{(\sqrt{5}a)^{2}-(\frac{3\sqrt{2}a}{2})^{2}}$=$\frac{\sqrt{2}a}{2}$,
∴tanBO′E=$\frac{BE}{O′E}=\frac{\frac{3\sqrt{2}a}{2}}{\frac{\sqrt{2}a}{2}}=3$,
∴tan∠BOD=3,
故答案为:3.
点评 本题考查解直角三角形,解答本题的关键是明确题意,作出合适的辅助线,利用勾股定理和等积法解答.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
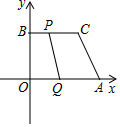 如图,在平面直角坐标系中,点A、B的坐标分别为(a,0)、(0,b),其中a、b满足|a+b-34|+|-a+b+18|=0,将点B向右平移24个单位得到点C.
如图,在平面直角坐标系中,点A、B的坐标分别为(a,0)、(0,b),其中a、b满足|a+b-34|+|-a+b+18|=0,将点B向右平移24个单位得到点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是抛物线y=ax2+bx+c(a≠0),其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论:
如图是抛物线y=ax2+bx+c(a≠0),其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com