
 .
.
 )
)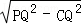 =
= =4,
=4,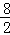 =4秒,点Q到达终点所需时间为
=4秒,点Q到达终点所需时间为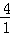 =4秒,
=4秒, ,即
,即 ,解得CE=
,解得CE= .
.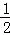 (OA+CF)•OC+
(OA+CF)•OC+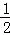 CF•CE﹣
CF•CE﹣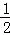 OA•OE=
OA•OE=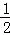 ×8+
×8+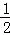 (8﹣t)•
(8﹣t)• ﹣
﹣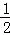 ×4×(8+
×4×(8+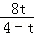 )
) ,即
,即 ,
, ,t2=6﹣2
,t2=6﹣2 ,
, 不符合题意,舍去.
不符合题意,舍去. )秒时,四边形APQF是梯形.
)秒时,四边形APQF是梯形.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,y1)、N(
,y1)、N( ,y2)、P(
,y2)、P( ,y3)三点都在函数
,y3)三点都在函数 (
( )的图象上,则yl、y2、y3的大小关系是( )
)的图象上,则yl、y2、y3的大小关系是( )| A.y2>y3>y1 | B.y2>y1>y3 | C.y3>y1>y2 | D.y3>y2>y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com