
分析 先设数据x1,x2,x3,x4,x5的平均数为$\overline{x}$,由方差S2=$\frac{1}{3}$,则另一组新数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数为3$\overline{x}$-2,方差为S′2,代入公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],计算即可.
解答 解:设数据x1,x2,x3,x4,x5的平均数为$\overline{x}$,则另一组新数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数为3$\overline{x}$-2,
∵S2=$\frac{1}{5}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(x5-$\overline{x}$)2]=$\frac{1}{3}$,
∴方差为S′2=$\frac{1}{5}$[(3x1-2-3$\overline{x}$+2)2+(3x2-2-3$\overline{x}$+2)2+…+(3x5-2-3$\overline{x}$+2)2]
=$\frac{1}{5}$[9(x1-$\overline{x}$)2+9(x2-$\overline{x}$)2+…+9(x5-$\overline{x}$)2]
=$\frac{1}{3}$×9
=3,
故答案为3.
点评 本题考查了方差的知识,说明了当数据都加上一个数(或减去一个数)时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数(或除以一个数)时,平均数也乘以或除以这个数,方差变为这个数的平方倍.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
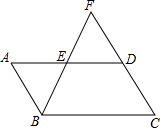 如图,?ABCD中,E为AD的中点,BE、CD相交于点F.
如图,?ABCD中,E为AD的中点,BE、CD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
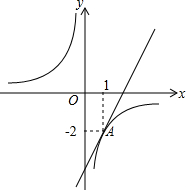 如图,直线y=2x+b与双曲线y=$\frac{k}{x}$(k≠0)只有一个公共点A(1,-2).
如图,直线y=2x+b与双曲线y=$\frac{k}{x}$(k≠0)只有一个公共点A(1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
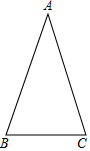 已知等腰△ABC的顶角∠A=36°(如图).
已知等腰△ABC的顶角∠A=36°(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
| 销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
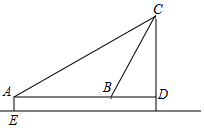 衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)
衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在E处用高为1.5米的测角仪AE,测得塔顶C的仰角为30°,再向塔身前进10.4米,又测得塔顶C的仰角为60°,求来雁塔的高度.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
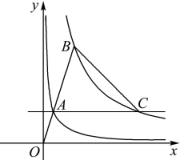 如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.
如图,分别位于反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$在第一象限图象上的两点A、B,与原点O在同一直线上,且$\frac{OA}{OB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com