
【题目】如图1,已知△ABC和△EFC都是等边三角形,且点E在线段AB上.

(1)求证:BF∥AC;
(2)过点E作EG∥BC交AC于点G,试判断△AEG的形状并说明理由;
(3)如图2,若点D在射线CA上,且ED=EC,求证:AB=AD+BF.
【答案】(1)见解析;(2)△AEG是等边三角形;理由见解析;(3)见解析.
【解析】
(1)如图1,根据等边三角形的性质得到∠ACB=∠ECF=60°,AC=BC,CE=FC,推出△ACE≌△FCB,得到∠CBF=∠A=60°,于是得到∠CBF =∠ACB,根据平行线的判定定理即可得到AC∥BF;
(2)过E作EG∥BC交AC于G,根据等边三角形的判定定理可证明△AEG是等边三角形;
(3)由(2)可知∠DAE=∠EGC=120°,可证明△ADE≌△GCE,进而得到AD=CG,再由(1)BF=AE=AG,于是可证得AB=BF+AD.
解:(1)如图1,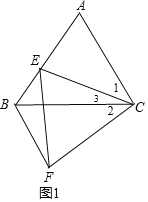
∵△ABC和△EFC都是等边三角形,
∴∠ACB=∠ECF=∠A= 60°,AC=BC,CE=FC,
∴∠1+∠3=∠2+∠3,
∴∠1=∠2,
在△ACE与△FCB中,
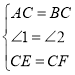 ,
,
∴△ACE≌△FCB,
∴∠CBF=∠A =60°,
∴∠CBF =∠ACB,
∴AC∥BF;
(2)△AEG是等边三角形,理由如下:
如图,过E作EG∥BC交AC于G,
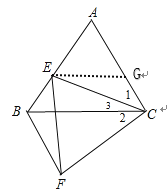
∵∠ABC=∠ACB=60°,
∴∠AEG=∠AGE=60°,
∴△AEG是等边三角形.
(3)如图2,过E作EG∥BC交AC于G,
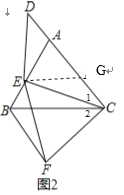
由(2)可知△AEG是等边三角形,
∴AE=EG=AG,∠GAE=∠AGC=60°,
∴∠DAE=∠EGC=120°,
∵DE=CE,
∴∠D=∠1,
∴△ADE≌△GCE,
∴AD=CG,
∴AC=AG+CG=AG+AD,
由(1)得△ACE≌△FCB,
∴BF=AE,
∴BF=AG,
∴AC=BF+AD,
∴AB=BF+AD.


科目:初中数学 来源: 题型:
【题目】为规范学生的在校表现,某班实行了操行评分制,根据学生的操行分高低分为A、B、C、D四个等级.现对该班上学期的操行等级进行了统计,并绘制了不完整的两种统计图,请根据图象回答问题:
(1)该班的总人数为_____人,得到等级A的学生人数在扇形统计图中的圆心角度数是_____;
(2)补全条形统计图;
(3)已知男生小伟和女生小颖的操行等级都是A,且获得等级A的学生中有2名男生,现班主任打算从操行等级为A的男生和女生中各任意抽取一名作为代表,参加学校的年度表彰大会,请用树状图或列表法求出抽到的代表中有小伟或小颖的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知M1(3,2),N1(5,-1),线段M1N1平移至线段MN处(注:M1与M,N1与N分别为对应点).
(1)若M(-2,5),请直接写出N点坐标.
(2)在(1)问的条件下,点N在抛物线![]() 上,求该抛物线对应的函数解析式.
上,求该抛物线对应的函数解析式.
(3)在(2)问条件下,若抛物线顶点为B,与y轴交于点A,点E为线段AB中点,点C(0,m)是y轴负半轴上一动点,线段EC与线段BO相交于F,且OC︰OF=2︰![]() ,求m的值.
,求m的值.
(4)在(3)问条件下,动点P从B点出发,沿x轴正方向匀速运动,点P运动到什么位置时(即BP长为多少),将△ABP沿边PE折叠,△APE与△PBE重叠部分的面积恰好为此时的△ABP面积的![]() ,求此时BP的长度.
,求此时BP的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在吴中区上方山动物园里有两只猴子在一棵树CD上的点B 处,且BC=5m,它们都要到池塘A处吃东西,其中一只猴子甲沿树爬至C再沿CA 走到离树24m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处.已知猴子甲所经过的路程比猴子乙所经过的路程多2m,设BD为xm.

(1)请用含有x的整式表示线段AD的长为 m;
(2)求这棵树高有多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小兰用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点DE为圆心,大于DE的一半长为半径作弧两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K使K和B在AC的两侧;
所以BH就是所求作的高.其中顺序正确的作图步骤是( )

A.①②③④B.④③①②C.②④③①D.④③②①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com