
分析 按照有理数混合运算的顺序,先乘除最后算加减,有括号的先算括号里面的.注意运用乘法的分配律简便计算.
解答 解:(-24)×($\frac{5}{12}-\frac{1}{8}$)-36$÷(\frac{1}{6}-\frac{1}{3})$
=-24×$\frac{5}{12}$+24×$\frac{1}{8}$-36÷(-$\frac{1}{6}$)
=-10+3+216
=209.
故答案为:209.
点评 本题考查的是有理数的运算能力.注意:
(1)要正确掌握运算顺序,在混合运算中要特别注意运算顺序:先三级,后二级,再一级;有括号的先算括号里面的;同级运算按从左到右的顺序;
(2)去括号法则:--得+,-+得-,++得+,+-得-.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
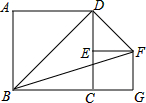 如图,菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上,点E在线段CD上,AB=2,∠ABC=60°,则△BDF的面积为( )
如图,菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上,点E在线段CD上,AB=2,∠ABC=60°,则△BDF的面积为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(2,0),与y轴交于点C(0,-2).
已知抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(2,0),与y轴交于点C(0,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com