已知等腰三角形的两边分别为3和6．
（1）求这个三角形的周长；
（2）若（1）中等腰三角形的顶角的外角平分线所在的直线与底角的外角平分线所在的直线交于P点，探索锐角∠P与原等腰三角形顶角的关系．
解：（1）当3为底时，三角形的三边长为3，6，6，则周长为15，
当3为腰时，三角形的三边长为3，3，6，则不能组成三角形，
故周长为15，
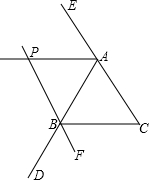
（2）相等，
∠BAC+2∠ABC=180°，
∠DBF=∠PBA=
（180°-∠ABC），
∠PAB=
（180°-∠BAC），
（2）∠P=90°-
∠A，
∵AB=AC，AP为∠EAB的角平分线，
∴∠B=∠C，∠EAP=∠PAB，
∵∠B+∠C+∠BAC=180°，
∠EAP+∠PAB+∠BAC=180°，
∴∠B+∠C=∠EAP+∠PAB，
∴∠B=∠PAB，
∴AP∥CB，
同理PF∥AC，
∴四边形APBC为平行四边形，
∴∠P=∠C=
（180°-∠A）=90°-
∠A．
分析：（1）分两种情况：当3为底时和3为腰时，再根据三角形的三边关系定理：两边之和大于第三边去掉一种情况即可，
（2）根据等腰三角形的性质和角平分线的性质求得∠ABC=∠PAB，从而得出AP∥CB，同理PF∥AC，根据平行四边形的性质即可得出答案．
点评：本题考查了等腰三角形的性质、三角形的三边关系定理以及平行四边形的性质，难度适中．
