
 如图,菱形ABCD中,∠DAB=60°,DF⊥AB于点E,且DF=DC,连结PC,则∠DCF的度数为45度.
如图,菱形ABCD中,∠DAB=60°,DF⊥AB于点E,且DF=DC,连结PC,则∠DCF的度数为45度. 分析 根据菱形的性质得出AD=AB,∠ADB=∠CDB=$\frac{1}{2}$∠ADC,AB∥DC,求出∠ADC=120°,△ADB是等边三角形,求出AD=BD,求出∠BDF=30°,求出△FDC是等腰直角三角形,即可求出答案.
解答 解:∵四边形ABCD是菱形,
∴AD=AB,∠ADB=∠CDB=$\frac{1}{2}$∠ADC,AB∥DC,
∵∠DAB=60°,
∴∠ADC=120°,
∴∠ADB=∠CDB=60°,
∵AD=AB,∠DAB=60°,
∴△ADB是等边三角形,
∴AD=BD,
∵DF⊥AB,
∴∠ADF=∠BDF=30°,
∴∠FDC=30°+60°=90°,
∵DF=DC,
∴∠DCF=∠DFC=45°,
故答案为:45.
点评 本题考查了菱形的性质,等边三角形的性质和判定,等腰直角三角形等知识点,能求出△FDC是等腰直角三角形是解此题的关键.


科目:初中数学 来源: 题型:选择题
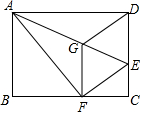 如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )
如图,将矩形ABCD沿AE折叠,点D的对应点落在BC上点F处,过点F作FG∥CD,连接EF,DG,下列结论中正确的有( )| A. | ①②③④ | B. | ①②③ | C. | ①③④ | D. | ①② |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{频数}{组距}$ | B. | $\frac{频率}{组距}$ | C. | $\frac{频率}{组数}$ | D. | $\frac{频数}{组数}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>1 | B. | m≥-1 | C. | m>-1且m≠0 | D. | m≥-1且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
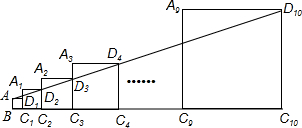 已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,Dn+1都在同一直线上,则正方形AnCnCn+1Dn+1的边长是$\frac{{3}^{n-1}}{{2}^{n-2}}$.
已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,Dn+1都在同一直线上,则正方形AnCnCn+1Dn+1的边长是$\frac{{3}^{n-1}}{{2}^{n-2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
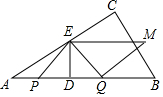 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=30,动点P、Q分别从点A、B同时出发,点P以10m/s的速度沿A→B向终点B运动,点Q以20m/s的速度沿B→A向终点A运动,过PQ的中点D作DE⊥AB交AC于点E,将△PQE绕着ED的中点旋转180°得到△MEQ,设四边形PQME的面积为S(cm2),点P运动的时间为t(s)
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=30,动点P、Q分别从点A、B同时出发,点P以10m/s的速度沿A→B向终点B运动,点Q以20m/s的速度沿B→A向终点A运动,过PQ的中点D作DE⊥AB交AC于点E,将△PQE绕着ED的中点旋转180°得到△MEQ,设四边形PQME的面积为S(cm2),点P运动的时间为t(s)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是3$\sqrt{2}$cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com