
【题目】如图,已知□AOBC的顶点O(0,0),![]() ,点B(12,0),按以下步骤作图:①以点O为圆心、适当长度为半径作弧,分别交OA、OB于点D,E;②分别以点D,E为圆心、大于
,点B(12,0),按以下步骤作图:①以点O为圆心、适当长度为半径作弧,分别交OA、OB于点D,E;②分别以点D,E为圆心、大于![]() 的长为半径作弧,两弧∠AOB在内交于点F;③作射线OF,交边AC于点G,则CG的长为( )
的长为半径作弧,两弧∠AOB在内交于点F;③作射线OF,交边AC于点G,则CG的长为( )

A.6B.7C.8D.9
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
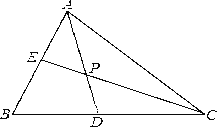
【题目】如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P
(1) 求∠CPD的度数
(2) 若AE=3,CD=7,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
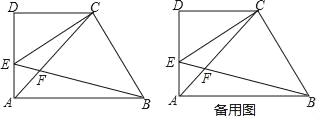
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“学习强国”阅读知识竞赛中,有901班和902班两个班参加比赛且人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分和70分.年级组长李老师将901班和902班的成绩进行整理并绘制成如下的统计图:
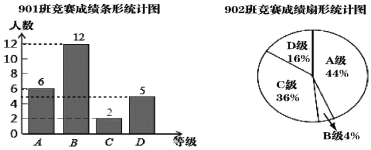
平均数(分) | 中位数(分) | 众数(分) | B级及以上人数 | |
901班 | 87.6 | 90 | 18 | |
902班 | 87.6 | 100 |
(1)在本次竞赛中,902班C级及以上的人数有多少?
(2)请你将表格补充完整:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,青少年用电脑手机过多,视力水平下降已引起了全社会的关注,某校为了解八年级1000名学生的视力情况,从中抽查了150名学生的视力情况,通过数据处理,得到如下的频数分布表.解答下列问题:
视力范围分组 | 组中值 | 频数 |
3.95≤x<4.25 | 4.1 | 20 |
4.25≤x<4.55 | 4.4 | 10 |
4.55≤x<4.85 | 4.7 | 30 |
4.85≤x<5.15 | 5.0 | 60 |
5.15≤x<5.45 | 5.3 | 30 |
合计 | 150 |
(1)分别指出参加抽测学生的视力的众数、中位数所在的范围;
(2)若视力为4.85以上(含4.85)为正常,试估计该校八年级学生视力正常的人数约为多少?
(3)根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数相应组中的权.请你估计该校八年级学生的平均视力是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
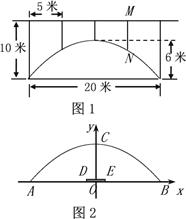
【题目】一座拱桥的截面轮廓为抛物线型(如图1),拱高6米,跨度20米,相邻两支柱间的距离均为5米.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是![]() 的形式. 请根据所给的数据求出
的形式. 请根据所给的数据求出![]() 的值.
的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间DE是一条宽2米的隔离带),其中的一条行车道能否并排行驶宽2米、高3米的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮与小明做投骰子(质地均匀的正方体)的实验与游戏.
(1)在实验中他们共做了50次试验,试验结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
填空:此次实验中,“1点朝上”的频率是 ;
② 小亮说:“根据试验,出现1点朝上的概率最大.”他的说法正确吗?为什么?
(2)小明也做了大量的同一试验,并统计了“1点朝上”的次数,获得的数据如下表:
试验总次数 | 100 | 200 | 500 | 1000 | 2000 | 5000 | 10000 |
1点朝上的次数 | 18 | 34 | 82 | 168 | 330 | 835 | 1660 |
1点朝上的频率 | 0.180 | 0.170 | 0.164 | 0.168 | 0.165 | 0.167 | 0.166 |
“1点朝上”的概率的估计值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=1,DE=3,∠EFB′=60°,则矩形ABCD的面积是( )
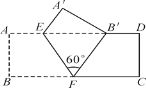
A.4B.8C.3![]() D.4
D.4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com