-$\sqrt{2}$的绝对值等于$\sqrt{2}$,$\sqrt{3}$的相反数等于-$\sqrt{3}$,$\sqrt{5}$的倒数等于$\frac{\sqrt{5}}{5}$．题目和参考答案——青夏教育精英家教网—

12．-$\sqrt{2}$的绝对值等于$\sqrt{2}$；$\sqrt{3}$的相反数等于-$\sqrt{3}$；$\sqrt{5}$的倒数等于$\frac{\sqrt{5}}{5}$．

分析根据绝对值的性质，相反数的意义，倒数的定义，可得答案．

解答解：-$\sqrt{2}$的绝对值等于 $\sqrt{2}$；$\sqrt{3}$的相反数等于-$\sqrt{3}$；$\sqrt{5}$的倒数等于 $\frac{\sqrt{5}}{5}$，
故答案为：$\sqrt{2}$，-$\sqrt{3}$，$\frac{\sqrt{5}}{5}$．

点评本题考查了实数的性质，利用绝对值的性质，相反数的意义，倒数的定义是解题关键．

练习册系列答案

开心语文现代文阅读技能训练100篇系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

2．下列事件中是必然事件的是（　　）

	A．	任意掷一枚硬币，落地后正面和反面同时朝上
	B．	李阿姨申请了北京市小客车购买指标，在申请后的第一次“摇号”时就中签
	C．	分别从写有2、4、5三个数字的三张卡片中随机抽出一张，卡片上的数字一定能被2整除
	D．	哥哥的年龄比弟弟大．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

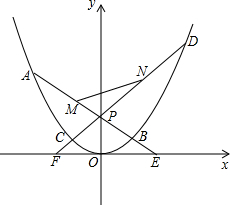抛物线C₀的顶点为原点O，且过点G（2，1）．如图，过点P（0，2）分别作两条直线，l₁：y=k₁x+2和l₂：y=k₂x+2（其中k₁•k₂≠0），两直线分别与抛物线、x轴相交于点A、B、E和D、C、F，且M、N分别是AB、CD的中点．
（1）求抛物线C₀的方程；
（2）若l₁⊥l₂，试分别用k₁、k₂表示E、F的坐标，并据此探究k₁、K₂满足的等量关系；
（3）若k₁+k₂=0，AP=2PB，求线MN的长．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

20．双曲线y=$\frac{k}{x}$位于第二、第四象限，则下面说法正确的是（　　）

	A．	y随x的增大而增大		B．	y随x的增大而减小
	C．	k＞0		D．	k＜0

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

7．下列格式中正确的是（　　）

A．

$\sqrt{25}$=±$\sqrt{5}$

B．

（-$\sqrt{0.36}$）²=-0.36

C．

$\root{3}{64}$=4

D．

$\sqrt{（-3）^{2}}$=3

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．

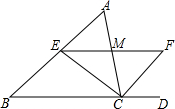如图，△ABC中，CE、CF分别是∠ACB及外角∠ACD的平分线，且CE交AB于点E，EF交AC于点M，已知EF∥BC．
（1）求证：M为EF中点；
（2）若∠B=40°，∠A=60°，求∠F的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

4．如图1，将两个完全相同的三角形纸片ABC和DEC如图1放置，点D在AB边上，其中∠ACB=∠DCE=90°，∠B=∠DEC=30°．

（1）操作发现
连接AE，设△BDC的面积为S₁，△AEC的面积为S₂，则S₁与S₂的数量关系是S₁=S₂．
（2）猜想论证
当这两个完全相同的三角形纸片ABC和DEC如图2放置时，连接AE和BD，（1）中S₁与S₂的数量关系仍然成立吗？请说明理由．
（3）拓展探究
已知∠ABC=60°，点D是∠ABC角平分线上一点，BD=CD=4$\sqrt{3}$，DE=4，BC=12，DE∥AB交BC于点E且DE=4（如图3）．若在射线BA上存在点F，使S_△DCF=S_△BDE，请求出相应的BF的长．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．石墨烯是世界上目前最薄却也最坚硬的纳米材料，还是导电性最好的材料，其理论厚度仅为0.00000000034米，该厚度用科学记数法表示为（　　）

A．

0.34×10^-9米

B．

34.0×10^-11米

C．

3.4×10^-10米

D．

3.4×10^-9米

查看答案和解析>>