
【题目】已知:在△ABC中,∠ABC=60°,CD平分∠ACB交AB于点D,点E在线段CD上(点E不与点C. D重合),且∠EAC=2∠EBC.

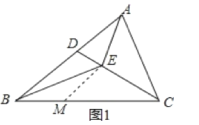
(1)如图1,若∠EBC=27°,且EB=EC,则∠DEB=___°,∠AEC=___°.
(2)如图2,①求证:AE+AC=BC;
②若∠ECB=30°,且AC=BE,求∠EBC的度数。
【答案】(1)27°,99°;(2)①见解析;②20°;
【解析】
(1)由等腰三角形的性质得到∠EBC=∠ECB=27°,根据角平分线的性质得到∠DEB=∠EBC+∠ECB=54°,再由角平分线的性质得到∠ACD=∠ECB=27°,因为∠EAC=2∠EBC=54°,求得∠AEC=180°-27°-54°=99°;
(2)①在BC上取一点M,使BM=ME,根据等腰三角形的性质得到∠MBE=∠MEB,由∠EAB=2∠MBE,∠EMC=∠MBE+∠MEB=2∠MBE,得到∠EAC=∠EMC,由全等三角形的性质推出AE=ME,CM=AC,于是得到结论;
②如图2,在BC上取一点M,使BM=ME,连接AM,由∠ECB=30°,得到∠ACB=60°,于是推出△AMC是等边三角形,通过三角形全等得到∠EBC=∠MAE,由∠MAC=60°,得到∠EAC=2∠EBC=2∠MAE,于是得出结果.
(1)∵EB=EC,
∴∠EBC=∠ECB=27°,
∵CD平分∠ACB,
∴∠ACD=∠ECB=27°,
∵∠EAC=2∠EBC=54°,
∴∠AEC=180°27°54°=99°,
故答案为:27°,99°;
(2)①证明:如图1,在BC上取一点M,使BM=ME,
∴∠MBE=∠MEB,
∵∠EAC=2∠MBE,∠EMC=∠MBE+∠MEB=2∠MBE,
∴∠EAC=∠EMC,
在△ACE与△MCE中,
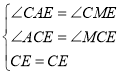 ,
,
∴△ACE≌△MCE,
∴AE=ME,CM=AC,
∴AE=BM,
∴BC=BM+CM=AE+AC;
②如图2在BC上取一点M,使BM=ME,连接AM,
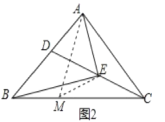
∵∠ECB=30°,
∴∠ACB=60°,由①可知;△AMC是等边三角形(M点与B点重合),
∴AM=AC=BE,
在△EMB与△MEA中,
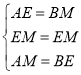 ,
,
∴∠EBC=∠MAE,
∵∠MAC=60°,
∵∠EAC=2∠EBC=2∠MAE,
∴∠MAE=20°,∠EAC=40°,
∴∠EBC=20°.


科目:初中数学 来源: 题型:
【题目】我市从 2018 年 1 月 1 日开始,禁止燃油助力车上路,于是电动自 行车的市场需求量日渐增多.某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)求 A、B 两种型号电动自行车的进货单价;
(2)若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)该商店如何进货才能获得最大利润?此时最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 轴和
轴和![]() 轴上的一动点.
轴上的一动点.

(1)如图![]() ,若点
,若点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)如图![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,
,![]() 平分
平分![]() ,若点
,若点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)如图![]() ,分别以
,分别以![]() 、
、![]() 为直角边在第三、四象限作等腰直角
为直角边在第三、四象限作等腰直角![]() 和等腰直角
和等腰直角![]() ,
,![]() 交
交![]() 轴于
轴于![]() ,若
,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,直线l:y=![]() x﹣
x﹣![]() 与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=
与x轴交于点A,经过点A的抛物线y=ax2﹣3x+c的对称轴是x=![]() .
.
(1)求抛物线的解析式;
(2)平移直线l经过原点O,得到直线m,点P是直线m上任意一点,PB⊥x轴于点B,PC⊥y轴于点C,若点E在线段OB上,点F在线段OC的延长线上,连接PE,PF,且PE=3PF.求证:PE⊥PF;
(3)若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE⊥PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
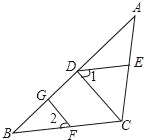
【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列小金鱼图案是用长度相同的小木棒按一定规律拼搭而成,第一条小金鱼图案需8根小木棒,第二条小金鱼图案需14根小木棒,…,按此规律,
(1)第n条小金鱼图案需要小木棒 根;
(2)如果有30000根小木棒,按照如图所示拼搭第1条,第2条……,直到第100条金鱼,请通过计算说明这些木棒是否够用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_______(只填写序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com