
分析 (1)根据解方程组,可得答案;
(2)根据x△y=ax+by(a、b是常数),可得答案.
解答 解:(1)由题意,得
$\left\{\begin{array}{l}{2a+3b=11}\\{5a-3b=10}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=3}\\{b=\frac{5}{3}}\end{array}\right.$;
(2)(-2)△$\frac{3}{5}$=-2a+$\frac{3}{5}$b=-2×3+$\frac{3}{5}$×$\frac{5}{3}$=-5.
点评 本题考查了解二元一次方程组,利用“x△y=ax+by(a、b是常数)”得出方程组是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
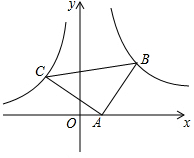 如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点C在双曲线y=-$\frac{4}{x}$(x<0)上,点A在x轴的正半轴上,且△ABC是以BC为斜边的等腰直角三角形.
如图,点B(3,3)在双曲线y=$\frac{k}{x}$(x>0)上,点C在双曲线y=-$\frac{4}{x}$(x<0)上,点A在x轴的正半轴上,且△ABC是以BC为斜边的等腰直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论::①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC,∠BAC=120°时,四边形AEFD是正方形.其中正确的结论是①②.(请写出正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
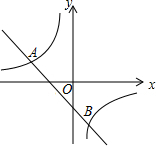 如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)交于点A(-4,n)和点B(2,-4).
如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)交于点A(-4,n)和点B(2,-4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
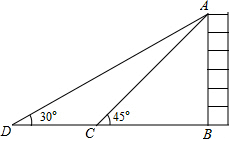 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.
如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为137米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尺规作图(不写作法,保留作图痕迹):
尺规作图(不写作法,保留作图痕迹):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com