
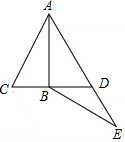
 如图,已知△ACD是等边三角形,AB是△ACD的中线,延长AD到点E,使得AB=BE.求证:BD=ED.
如图,已知△ACD是等边三角形,AB是△ACD的中线,延长AD到点E,使得AB=BE.求证:BD=ED.  口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 图中的容量器是两个形状、大小相同、高度相等都为Hdm的圆台形容器构成,若往此容器中注水,设注入容器中水的高度为h(dm),注水时间为t(s),则h关于t的函数图象是( )
图中的容量器是两个形状、大小相同、高度相等都为Hdm的圆台形容器构成,若往此容器中注水,设注入容器中水的高度为h(dm),注水时间为t(s),则h关于t的函数图象是( )| A. | 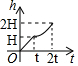 | B. | 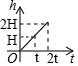 | C. | 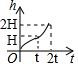 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
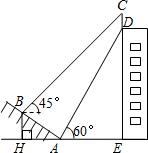 如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH=$\frac{1}{2}$,AB=10米,AE=15米.
如图,某大楼的顶部有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知sin∠BAH=$\frac{1}{2}$,AB=10米,AE=15米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com