
،¾جâؤ؟،؟شؤ¶ء²ؤءد£؛
خزأاضھµہ£؛ز»جُض±دك¾¹µبرüض±½اب½اذخµؤض±½ا¶¥µم£¬¹ءيحâء½¸ِ¶¥µم·ض±ًدٍ¸أض±دك×÷´¹دك£¬¼´؟ةµأب´¹ض±ؤ£ذح،±بçح¼¢ظ£¬شع![]() ضذ£¬
ضذ£¬![]() £¬
£¬![]() £¬·ض±ً¹
£¬·ض±ً¹![]() ،¢
،¢![]() دٍ¾¹µم
دٍ¾¹µم![]() ض±دك×÷´¹دك£¬´¹×م·ض±ًخھ
ض±دك×÷´¹دك£¬´¹×م·ض±ًخھ![]() ،¢
،¢![]() £¬خزأا؛ـبفز×·¢دض½لآغ£؛
£¬خزأا؛ـبفز×·¢دض½لآغ£؛![]() £®
£®
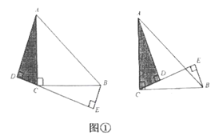
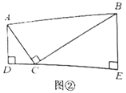

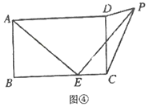
£¨1£©ج½¾؟ختجâ£؛بç¹û![]() £¬ئنثûجُ¼²»±ن£¬بçح¼¢ع£¬؟ةµأµ½½لآغ£»
£¬ئنثûجُ¼²»±ن£¬بçح¼¢ع£¬؟ةµأµ½½لآغ£»![]() £®اëؤمثµأ÷ہيسة£®
£®اëؤمثµأ÷ہيسة£®
£¨2£©ر§زشضآسأ£؛بçح¼¢غ£¬شعئ½أوض±½ا×ّ±êدµضذ£¬ض±دك![]() سëض±دك
سëض±دك![]() ½»سعµم
½»سعµم![]() £¬ازء½ض±دك¼ذ½اخھ
£¬ازء½ض±دك¼ذ½اخھ![]() £¬از
£¬از![]() £¬اëؤماَ³ِض±دك
£¬اëؤماَ³ِض±دك![]() µؤ½âخِت½£®
µؤ½âخِت½£®
£¨3£©حطص¹س¦سأ£؛بçح¼¢ـ£¬شع¾طذخ![]() ضذ£¬
ضذ£¬![]() £¬
£¬![]() £¬µم
£¬µم![]() خھ
خھ![]() ±كةد،ھ¸ِ¶¯µم£¬ء¬½س
±كةد،ھ¸ِ¶¯µم£¬ء¬½س![]() £¬½«دك¶خ
£¬½«دك¶خ![]() بئµم
بئµم![]() ث³ت±صëذ×ھ
ث³ت±صëذ×ھ![]() £¬µم
£¬µم![]() آنشعµم
آنشعµم![]() ´¦£¬µ±µم
´¦£¬µ±µم![]() شع¾طذخ
شع¾طذخ![]() حâ²؟ت±£¬ء¬½س
حâ²؟ت±£¬ء¬½س![]() £¬
£¬![]() £®بô
£®بô![]() خھض±½اب½اذخت±£¬اëؤمج½¾؟²¢ض±½سذ´³ِ
خھض±½اب½اذخت±£¬اëؤمج½¾؟²¢ض±½سذ´³ِ![]() µؤ³¤£®
µؤ³¤£®
،¾´ً°¸،؟£¨1£©ہيسة¼û½âخِ£»£¨2£©![]() £»£¨3£©
£»£¨3£©![]() ³¤خھ3»ٍ
³¤خھ3»ٍ![]() £®
£®
،¾½âخِ،؟
£¨1£©¸ù¾فح¬½اµؤسà½ادàµبµأµ½![]() £¬ب»؛َہûسأAA¶¨ہيإذ¶¨ب½اذخدàثئ£»
£¬ب»؛َہûسأAA¶¨ہيإذ¶¨ب½اذخدàثئ£»
£¨2£©¹µم![]() ×÷
×÷![]() ½»ض±دك
½»ض±دك![]() سعµم
سعµم![]() £¬·ض±ً¹
£¬·ض±ً¹![]() ،¢
،¢![]() ×÷
×÷![]() ضل£¬
ضل£¬![]() ضل£¬سة£¨1£©µأ
ضل£¬سة£¨1£©µأ![]() £¬´س¶ّµأµ½
£¬´س¶ّµأµ½![]() £¬ب»؛َ½ل؛ددàثئب½اذخµؤذشضت؛حبٌ½اب½ا؛¯تاَ³ِ
£¬ب»؛َ½ل؛ددàثئب½اذخµؤذشضت؛حبٌ½اب½ا؛¯تاَ³ِ![]() £¬
£¬![]() £¬´س¶ّب·¶¨Nµم×ّ±ê£¬ب»؛َہûسأ´¶¨دµت·¨اَ؛¯ت½âخِت½£»
£¬´س¶ّب·¶¨Nµم×ّ±ê£¬ب»؛َہûسأ´¶¨دµت·¨اَ؛¯ت½âخِت½£»
£¨3£©·ضء½ضضاéذخجضآغ£؛¢ظبçح¼1ضذ£¬µ±،دPDC=90،مت±£®¢عبçح¼2ضذ£¬µ±،دDPC=90،مت±£¬×÷PF،حBCسعF£¬PH،حCDسعH£¬ةèBE=x£®·ض±ًاَ½â¼´؟ة£®
½â£؛£¨1£©،ك![]() £¬،à
£¬،à![]()
سض،ك![]()
،à![]()
،à![]()
،ك![]() £®
£®
،à![]()
£¨2£©بçح¼£¬¹µم![]() ×÷
×÷![]() ½»ض±دك
½»ض±دك![]() سعµم
سعµم![]() £¬
£¬
·ض±ً¹![]() ،¢
،¢![]() ×÷
×÷![]() ضل£¬
ضل£¬![]() ضل
ضل
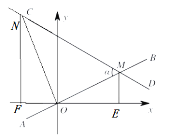
سة£¨1£©µأ![]() ،à
،à![]()
،ك![]() ×ّ±ê
×ّ±ê![]() ،à
،à![]() £¬
£¬![]()
،ك![]() ،à
،à![]()
½âµأ£؛![]() £¬
£¬![]() ،à
،à![]()
ةèض±دك![]() ±ي´ïت½خھ
±ي´ïت½خھ![]() £¬´ْبë
£¬´ْبë![]() £¬
£¬![]()
µأ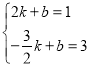 £¬½âµأ
£¬½âµأ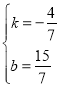 £¬
£¬
،àض±دك![]() ±ي´ïت½خھ
±ي´ïت½خھ![]()
£¨3£©½â£؛¢ظبçح¼1ضذ£¬µ±،دPDC=90،مت±£¬
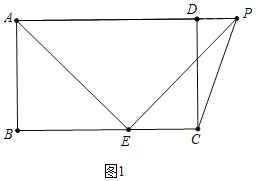
،ك،دADC=90،م£¬
،à،دADC+،دPDC=180،م£¬
،àA،¢D،¢P¹²دك£¬
،كEA=EP£¬،دAEP=90،م£¬
،à،دEAP=45،م£¬،ك،دBAD=90،م£¬
،à،دBAE=45،م£¬،ك،دB=90،م
،à،دBAE=،دBEA=45،م£¬
،àBE=AB=3£®
¢عبçح¼2ضذ£¬µ±،دDPC=90،مت±£¬×÷PF،حBCسعF£¬PH،حCDسعH£¬ةèBE=x£¬
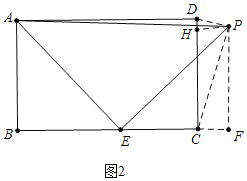
،ك،دAEB+،دPEF=90،م£¬،دAEB+،دBAE=90،م£¬
،à،دBAE=،دPEF£¬
شع،÷ABE؛ح،÷EFPضذ£¬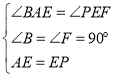
،à،÷ABE،ص،÷EFP£¬
،àEF=AB=3£¬PF=HC=BE=x£¬
،àCF=3-£¨5-x£©=x-2£¬
،ك،دDPH+،دCPH=90،م£¬،دCPH+،دPCH=90،م£¬
،à،دDPH=،دPCH£¬،ك،دDHP=،دPHC£¬
،à،÷PHD،×،÷CHP£¬
،àPH2=DHCH£¬
،ࣨx-2£©2=x£¨3-x£©£¬
،àx=![]() »ٍ
»ٍ![]() £¨ةلئْ£©£¬
£¨ةلئْ£©£¬
،àBE=![]() £¬
£¬
×غةدثùتِ£¬µ±،÷PDCتاض±½اب½اذخت±£¬BEµؤضµخھ3»ٍ![]() £®
£®


 أ؟بص10·ضضس؟عثمذؤثمثظثمجىجىء·دµءذ´ً°¸
أ؟بص10·ضضس؟عثمذؤثمثظثمجىجىء·دµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟خھ»¼«دىس¦ص¸®جل³ِµؤ،°آجة«·¢ص¹،¤µحج¼³ِذذ،±؛إصظ£¬ؤ³ةçاّ¾ِ¶¨¹؛ضأز»إْ¹²ديµ¥³µ£¬¾تذ³،µ÷²éµأضھ£¬¹؛آٍ3ء؟ؤذت½µ¥³µسë4ء¾إ®ت½µ¥³µ·رسأدàح¬£¬¹؛آٍ5ء¾ؤذت½µ¥³µسë4ء¾إ®ت½µ¥³µ¹²ذè16000شھ.
(1)اَؤذت½µ¥³µ؛حإ®ت½µ¥³µµؤµ¥¼غ£»
(2)¸أةçاّزھاَؤذت½µ¥±بإ®ت½µ¥³µ¶à4ء¾£¬ء½ضضµ¥³µضءةظذèزھ22ء¾£¬¹؛ضأء½ضضµ¥³µµؤ·رسأ²»³¬¹50000شھ£¬¸أةçاّسذ¼¸ضض¹؛ضأ·½°¸£؟شُرù¹؛ضأ²إؤـت¹ثùذè×ـ·رسأ×îµح£¬×îµح·رسأتا¶àةظ£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬±ك³¤خھ1µؤص·½ذخABCDبئµمAؤوت±صëذ×ھ30،مµ½ص·½ذخAB،¯C،¯D،¯£¬ح¼ضذزُس°²؟·ضµؤأو»خھ£¨ £©£®
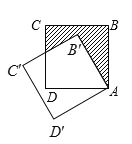
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شع»سذ·½¸ٌح¼µؤئ½أوض±½ا×ّ±êدµضذ£¬،÷ABCµؤب¸ِ¶¥µم¾ùشع¸ٌµمةد.
£¨1£©½«،÷ACBبئµمBث³ت±صë·½دٍذ×ھ![]() £¬شع·½¸ٌح¼ضذسأض±³ك»³ِذ×ھ؛َ¶شس¦µؤ،÷A1C1B£¬شٍA1µمµؤ×ّ±êتا£¨_________£©£¬C1µمµؤ×ّ±êتا£¨_________£©.
£¬شع·½¸ٌح¼ضذسأض±³ك»³ِذ×ھ؛َ¶شس¦µؤ،÷A1C1B£¬شٍA1µمµؤ×ّ±êتا£¨_________£©£¬C1µمµؤ×ّ±êتا£¨_________£©.
£¨2£©شع·½¸ٌح¼ضذسأض±³ك»³ِ،÷ACB¹طسعشµمOµؤضذذؤ¶ش³ئح¼ذخ،÷A2C2B2£¬شٍA2µمµؤ×ّ±êتا£¨_________£©£¬C2µمµؤ×ّ±êتا£¨_________£©.

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³؟عصض¼س¹¤³§سذ![]() ء½×鹤بث¹²
ء½×鹤بث¹²![]() بث£¬
بث£¬![]() ×鹤بثأ؟بثأ؟ذ،ت±؟ة¼س¹¤؟عصض
×鹤بثأ؟بثأ؟ذ،ت±؟ة¼س¹¤؟عصض![]() ض»£¬
ض»£¬![]() ×鹤بثأ؟بثأ؟ذ،ت±؟ة¼س¹¤؟عصض
×鹤بثأ؟بثأ؟ذ،ت±؟ة¼س¹¤؟عصض![]() ض»£¬
ض»£¬![]() ء½×鹤بثأ؟ذ،ت±ز»¹²؟ة¼س¹¤؟عصض
ء½×鹤بثأ؟ذ،ت±ز»¹²؟ة¼س¹¤؟عصض![]() ض»£®
ض»£®
£¨1£©اَ![]() ء½×鹤بث¸÷¶àةظبث£»
ء½×鹤بث¸÷¶àةظبث£»
£¨2£©سةسعزكاé¼سضط![]() ء½×鹤بث¾ùجل¸كءث¹¤×÷ذ§آت£¬ز»أû
ء½×鹤بث¾ùجل¸كءث¹¤×÷ذ§آت£¬ز»أû![]() ×鹤بث؛حز»أû
×鹤بث؛حز»أû![]() ×鹤بثأ؟ذ،ت±¹²؟ةةْ²ْ؟عصض
×鹤بثأ؟ذ،ت±¹²؟ةةْ²ْ؟عصض![]() ض»£¬بô
ض»£¬بô![]() ء½×鹤بثأ؟ذ،ت±ضءةظ¼س¹¤
ء½×鹤بثأ؟ذ،ت±ضءةظ¼س¹¤![]() ض»؟عصض£¬ؤاأ´
ض»؟عصض£¬ؤاأ´![]() ×鹤بثأ؟بثأ؟ذ،ت±ضءةظ¼س¹¤¶àةظض»؟عصض£؟
×鹤بثأ؟بثأ؟ذ،ت±ضءةظ¼س¹¤¶àةظض»؟عصض£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعئ½أوض±½ا×ّ±êدµضذ£¬ز»´خ؛¯تy=kx+bµؤح¼دَسëxضل½»سعµمA£¨©پ1£¬0£©£¬سë·´±بہ؛¯تy= ![]() شعµعز»دَدقؤعµؤح¼دَ½»سعµمB£¨
شعµعز»دَدقؤعµؤح¼دَ½»سعµمB£¨![]() £¬n£©£®ء¬½سOB£¬بôS،÷AOB=1£®
£¬n£©£®ء¬½سOB£¬بôS،÷AOB=1£®
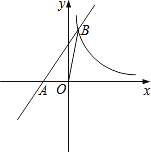
£¨1£©اَ·´±بہ؛¯تسëز»´خ؛¯تµؤ¹طدµت½£»
£¨2£©ض±½سذ´³ِ²»µبت½×é 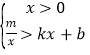 µؤ½â¼¯£®
µؤ½â¼¯£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
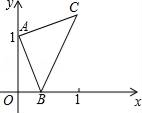
،¾جâؤ؟،؟بçسزح¼£¬µمAµؤ×ّ±êخھ£¨0£¬1£©£¬µمBتاxضلص°ëضلةدµؤز»¶¯µم£¬زشABخھ±ك×÷µبرüض±½ا،÷ABC£¬ت¹،دBAC=90،م£¬بç¹ûµمBµؤ؛ل×ّ±êخھx£¬µمCµؤ×ف×ّ±êخھy£¬ؤاأ´±يت¾yسëxµؤ؛¯ت¹طدµµؤح¼دٌ´َضآتا£¨ £©
A.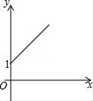 B.
B.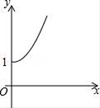
C.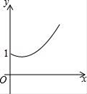 D.
D.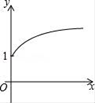
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
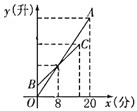
،¾جâؤ؟،؟ز»¸ِذîث®³طسذ¼×،¢ززء½¸ِ×¢ث®¹ـ؛حز»¸ِإإث®¹ـ±û£¬ب¸ِث®¹ـ¾ùزر¹ط±ص£¬زرضھزز×¢ث®¹ـµؤ×¢ث®ثظ¶بخھ10ة/·ض£®دب´ٍ؟ھزز×¢ث®¹ـ4·ضضس£¬شظ´ٍ؟ھ¼××¢ث®¹ـ£¬¼×،¢ززء½¸ِث®¹ـ¾ù×¢ث®20·ضضس£®ةè¼××¢ث®¹ـµؤ¹¤×÷ت±¼نخھ![]() £¨·ض£©£¬¼××¢ث®¹ـµؤ×¢ث®ء؟
£¨·ض£©£¬¼××¢ث®¹ـµؤ×¢ث®ء؟![]() £¨ة£©سëت±¼ن
£¨ة£©سëت±¼ن![]() £¨·ض£©µؤ؛¯تح¼دَخھدك¶خ
£¨·ض£©µؤ؛¯تح¼دَخھدك¶خ![]() £¬زز×¢ث®¹ـµؤ×¢ث®ء؟
£¬زز×¢ث®¹ـµؤ×¢ث®ء؟![]() £¨ة£©سëت±¼ن
£¨ة£©سëت±¼ن![]() £¨·ض£©µؤ؛¯تح¼دَخھدك¶خ
£¨·ض£©µؤ؛¯تح¼دَخھدك¶خ![]() £¬بçح¼ثùت¾£®
£¬بçح¼ثùت¾£®
£¨1£©اَ¼××¢ث®¹ـµؤ×ـ×¢ث®ء؟£»
£¨2£©اَدك¶خ![]() ثù¶شس¦µؤ؛¯ت¹طدµت½£¬²¢ذ´³ِ×ش±نء؟µؤب،ضµ·¶خ§£»
ثù¶شس¦µؤ؛¯ت¹طدµت½£¬²¢ذ´³ِ×ش±نء؟µؤب،ضµ·¶خ§£»
£¨3£©زز×¢ث®¹ـ´ٍ؟ھµؤ16·ضضس؛َ£¬´ٍ؟ھ±û³ِث®¹ـ£®زرضھ³ِث®¹ـ±ûµؤإإث®ثظ¶بخھ20ة/·ض£¬اَ±û³ِث®¹ـ´ٍ؟ھ¶à³¤ت±¼نؤـ½«ذîث®³طµؤث®إإ؟ص£®
²é؟´´ً°¸؛ح½âخِ>>
°ظ¶بضآذإ - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com