
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.

(1)当![]() 时,
时,![]() ______________
______________![]() ;点
;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变____________(填“大”或“小”);
逐渐变____________(填“大”或“小”);
(2)当![]() 时,求证:
时,求证:![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,判断当
的形状也在改变,判断当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形.
是等腰三角形.
【答案】(1)25°;小;(2)见解析;(3)当∠BDA的度数为80°或110°时,△ADE是等腰三角形.
【解析】
(1)利用三角形内角和定理,即可求出![]() ;然后根据∠BAD的变化情况,即可判断
;然后根据∠BAD的变化情况,即可判断![]() 的变化情况;
的变化情况;
(2)利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AAS即可得出△ABD≌△DCE;
(3)根据等腰三角形的腰的情况分类讨论,再利用等腰三角形的性质和三角形的外角即可分别求出∠BDA.
解:∵在△BAD中,∠B=40°,∠BDA=115°,
∴∠BAD=180°﹣∠B﹣∠BDA=25°;
∠BAD+∠BDA=180°﹣∠B=140°
由图可知:点![]() 从
从![]() 向
向![]() 运动时,∠BAD逐渐变大,则
运动时,∠BAD逐渐变大,则![]() 逐渐变小.
逐渐变小.
故答案为:25°;小;
(2)∵∠B=∠C=40°,
∴∠DEC+∠EDC=180°﹣∠C=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=180°﹣∠ADE =140°,
∴∠ADB=∠DEC,
∵![]() ,
,![]()
∴![]()
在△ABD和△DCE中,

∴△ABD≌△DCE(AAS).
(3)当△ADE是等腰三角形时,∠BDA的度数为80°或110°,
①当ED=EA时,
∴∠DAE=∠EDA=40°,
∴∠BDA=∠C+DAE=80°;
②当DA=DE时,
∴∠DAE=∠DEA=![]() (180°﹣∠ADE)=70°,
(180°﹣∠ADE)=70°,
∴∠BDA=∠C+DAE=110°,
③当AD=AE时,
∠ADE=∠AED=40°
∵∠C=40°
∠AED是△EDC的外角
∴∠AED>∠C,与∠AED=40°矛盾
所以此时不成立;
综上所述:当∠BDA的度数为80°或110°时,△ADE是等腰三角形.


科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
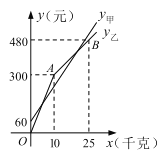
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴建立如图所示的平面直角坐标系,F是BC上的一个动点(不与B、C重合),过F点的反比例函数![]() (k>0)的图象与AC边交于点E,连接OE,OF,EF.
(k>0)的图象与AC边交于点E,连接OE,OF,EF.
(1)若tan∠BOF=![]() ,求F点的坐标;
,求F点的坐标;
(2)当点F在BC上移动时,△OEF与△ECF的面积差记为S,求当k为何值时,S有最大值,最大值是多少?
(3)是否存在这样的点F,使得△OEF为直角三角形?若存在,求出此时点F坐标;若不存在,请说明理由。
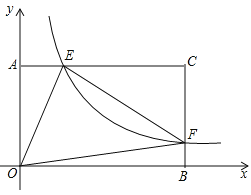
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次实验中,马达同学把一根弹簧的上端固定,在其下端悬挂物体质量![]() 的一组对应值.
的一组对应值.
所挂物体质量 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度 | 18 | 20 | 22 | 24 | 26 | 28 |
(1)上表反应了哪两个变量之间的关系,并指出谁是自变量,谁是因变量.
(2)当悬挂物体的重量为3千克时,弹簧长 ;不挂重物时弹簧长 .
(3)弹簧长度![]() 所挂物体质量
所挂物体质量![]() 之间的关系可以用式子表示为: .
之间的关系可以用式子表示为: .
(4)求挂![]() 物体时弹簧长度及弹簧长
物体时弹簧长度及弹簧长![]() 时所挂物体的重量.
时所挂物体的重量.
查看答案和解析>>
科目:初中数学 来源: 题型:
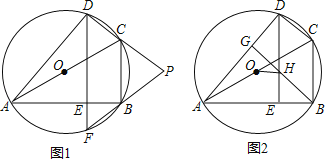
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,CA=CB, AG平分∠BAC交BC于H,BG⊥AG,垂足为G.若AH=8,则BG的长为( )
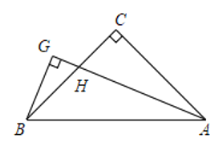
A.3B.5C.8D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结果如此巧合!
下面是小颖对一道题目的解答.
题目:如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.
解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.
根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.
整理,得x2+7x=12.
所以S△ABC=![]() ACBC
ACBC
=![]() (x+3)(x+4)
(x+3)(x+4)
=![]() (x2+7x+12)
(x2+7x+12)
=![]() ×(12+12)
×(12+12)
=12.
小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.
可以一般化吗?
(1)若∠C=90°,求证:△ABC的面积等于mn.
倒过来思考呢?
(2)若ACBC=2mn,求证∠C=90°.
改变一下条件……
(3)若∠C=60°,用m、n表示△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想我们曾经学习过的三角形外心的概念,我们可引入准外心的定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.请回答下面的三个问题:

(1)如图1,若PB=PC,则点P为△ABC的准外心,而且我们知道满足此条件的准外心有无数多个,你能否用尺规作出另外一个准外心Q呢?请尝试完成;
(2)如图2,已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长;
(3)如图3,点B既是△EDC又是△ADC的准外心,BD=BA=BC=2AD,BD∥AC,CD=![]() ,求AD的值.
,求AD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为![]() ,AC=2+2
,AC=2+2![]() ,则△CEF的面积为( )
,则△CEF的面积为( )

A. ![]() B. 2
B. 2![]() C. 2+
C. 2+![]() D. 2
D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com