
分析 直接利用二次根式乘除运算法则将原式变形求出答案.
解答 解:∵a>0,b>0,
∴$\frac{5}{b}$$\sqrt{a{b}^{5}}$•(-$\frac{3}{5}$$\sqrt{{a}^{3}b}$)÷($\frac{1}{3}$$\sqrt{\frac{b}{a}}$)
=-$\frac{5}{b}$×$\frac{3}{5}$×3$\sqrt{a{b}^{5}×{a}^{3}b×\frac{a}{b}}$
=-$\frac{9}{b}$×a2b2$\sqrt{ab}$
=-9a2b$\sqrt{ab}$.
点评 此题主要考查了二次根式的乘除运算,正确化简二次根式是解题关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
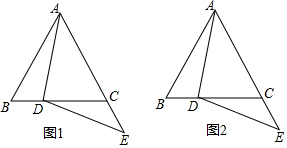 在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)
在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA(如图1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年北京市西城区七年级上学期期末考试数学试卷(解析版) 题型:解答题
阅读下列材料:
《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿。其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。凡百钱买鸡百只,问鸡翁、母、雏各几何。”

译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱。现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?
结合你学过的知识,解决下列问题:
(1)若设公鸡有x只,母鸡有y只,
①则小鸡有____________只,买小鸡一共花费____________文钱;(用含x,y的式子表示)
②根据题意列出一个含有x,y的方程: ______________________________;
(2)若对“百鸡问题”增加一个条件:公鸡数量是母鸡数量的3倍,求此时公鸡、母鸡、小鸡各有多少只?
(3)除了问题(2)中的解之外,请你再直接写出两组符合“百鸡问题”的解。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com