
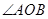 是一个直角,在角的内部作射线
是一个直角,在角的内部作射线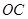 ,再分别作
,再分别作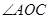 和
和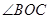 的平分线
的平分线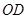 、
、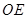 .
.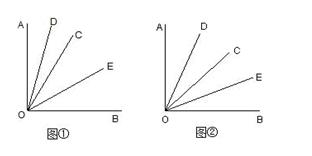
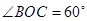 时,则求
时,则求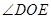 的度数;
的度数;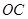 在
在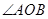 内绕
内绕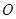 点旋转时,
点旋转时,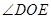 的大小是否发生变化?若变化,说明理由;若不变,求
的大小是否发生变化?若变化,说明理由;若不变,求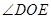 的度数.
的度数.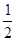 ∠BOC=30°,∠DOC=
∠BOC=30°,∠DOC=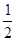 ∠AOC=15°,即可求得结果;
∠AOC=15°,即可求得结果;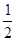 ∠BOC,∠DOC=
∠BOC,∠DOC=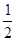 ∠AOC,则∠DOE=∠COE+∠COD=
∠AOC,则∠DOE=∠COE+∠COD=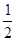 (∠BOC+∠AOC),得到∠DOE=
(∠BOC+∠AOC),得到∠DOE=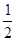 ∠AOB,即可计算出∠DOE的度数.
∠AOB,即可计算出∠DOE的度数.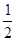 ∠BOC=30°,∠DOC=
∠BOC=30°,∠DOC=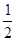 ∠AOC=15°,
∠AOC=15°,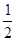 ∠BOC,∠DOC=
∠BOC,∠DOC=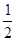 ∠AOC,
∠AOC,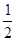 (∠BOC+∠AOC)=
(∠BOC+∠AOC)=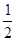 ∠AOB=
∠AOB=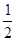 ×90°=45°.
×90°=45°.

科目:初中数学 来源:不详 题型:单选题
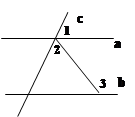
| A.110° | B.118° | C.132° | D.无法确定 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
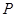 是
是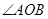 的边
的边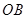 上的一点.
上的一点.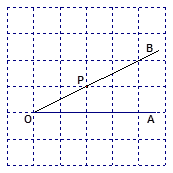
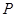 画OB的垂线,交
画OB的垂线,交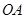 于点C;
于点C;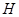 ;
;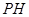 的长度是点
的长度是点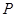 到直线 的距离, 是点
到直线 的距离, 是点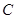 到直线
到直线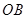 的距离;因为 ,所以线段
的距离;因为 ,所以线段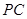 、
、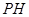 、
、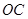 这三条线段大小关系是 (用“<”号连接)
这三条线段大小关系是 (用“<”号连接)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com