
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=![]() S△ABC;④EF=AP.上述结论始终正确的有( )
S△ABC;④EF=AP.上述结论始终正确的有( )
②③

A.①②③④B.①②③C.①③④D.②③④
【答案】B
【解析】
根据等腰直角三角形的性质得:AP⊥BC,AP=![]() BC,AP平分∠BAC.所以可证∠C=∠EAP;∠FPC=∠EPA;AP=PC.即证得△APE与△CPF全等.根据全等三角形性质判断结论是否正确.
BC,AP平分∠BAC.所以可证∠C=∠EAP;∠FPC=∠EPA;AP=PC.即证得△APE与△CPF全等.根据全等三角形性质判断结论是否正确.
∵∠APE、∠CPF都是∠APF的余角,
∴∠APE=∠CPF,
∵AB=AC,∠BAC=90°,P是BC中点,
∴AP=CP,
∴∠PAE=∠PCF,
在△APE与△CPF中,
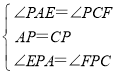 ,
,
∴△APE≌△CPF(ASA),
同理可证△APF≌△BPE,
∴AE=CF,△EPF是等腰直角三角形,S四边形AEPF=![]() S△ABC,①②③正确;
S△ABC,①②③正确;
而AP=![]() BC,当EF不是△ABC的中位线时,则EF不等于BC的一半,EF≠AP,
BC,当EF不是△ABC的中位线时,则EF不等于BC的一半,EF≠AP,
∴故④不成立.
故始终正确的是①②③.
故选:B.


科目:初中数学 来源: 题型:
【题目】五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为4的顶点开始,第2018次“移位”后,那么他所处的顶点的编号是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,三角形ABC的顶点坐标分别是A(0,0),B(5,0),C(4,4).
(1)将三角形ABC向上平移2个单位长度,再向右平移3个单位长度,得到三角形A1B1C1,请在直角坐标系中画平移后的三角形A1B1C1
(2)求三角形ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学校团委开展“关爱残疾儿童”爱心捐书活动,全校师生踊跃捐赠各类书籍共6000本.为了解各类书籍的分布情况,从中随机抽取了部分书籍分四类进行统计:A.艺术类;B.文学类;C.科普类;D.其他,并将统计结果绘制成如图所示的两幅不完整的统计图.
(1)这次统计共抽取了200____本书籍,扇形统计图中的m=40____,∠α的度数是___;
(2)请将条形统计图补充完整;
(3)估计全校师生共捐赠了多少本文学类书籍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
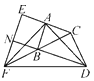
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求A,B两点间的距离(结果精确到0.1km).
(参考数据:sin34°=0.56,cos34°=0.83,tan34°=0.67.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令
,令![]() .
.
(1)若![]() 的函数图象相交于
的函数图象相交于![]() 轴上的同一点.
轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,
为何值时,![]() 的值最小,试求出该最小值.
的值最小,试求出该最小值.
(2)当![]() 时,
时,![]() 随
随![]() 的增大而减小,请写出
的增大而减小,请写出![]() 的大小关系并给予证明.
的大小关系并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com