
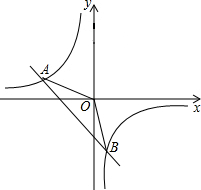
 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).分析 (1)根据点A的坐标利用反比例函数图象上点的坐标特征即可求出m值,从而得出反比例函数解析式;再由点B在反比例函数图象上,即可求出n值,根据A、B点的坐标利用待定系数法即可求出一次函数解析式;
(2)令一次函数解析式中x=0,求出y值,即可得出点C的坐标,从而得出OC的长,再利用分割图形求面积法结合三角形的面积公式即可求出S△AOB的值;
(3)观察两函数图象,根据两函数图象的上下位置关系结合交点的坐标即可找出不等式y1<y2<0的解集.
解答 解:(1)∵反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象过点A(-2,1),
∴m=-2×1=-2,
∴反比例函数解析式为y2=-$\frac{2}{x}$;
∵点B(1,n)在反比例函数y2=-$\frac{2}{x}$的图象上,
∴n=-2,即点B(1,-2).
将点A(-2,1)、B(1,-2)代入到y1=ax+b(a,b为常数,且a≠0)中,
得:$\left\{\begin{array}{l}{1=-2a+b}\\{-2=a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=-1}\end{array}\right.$,
∴一次函数解析式为y1=-x-1.
(2)令y1=-x-1中x=0,则y=-1,
∴点C(0,-1),OC=1.
∴S△AOB=$\frac{1}{2}$OC•(xB-xA)=$\frac{1}{2}$×1×[1-(-2)]=$\frac{3}{2}$.
(3)观察函数图象,发现:
在x轴的下方,当x>1时,一次函数图象在反比例函数图形的下方,
∴当y1<y2<0时,自变量x的取值范围为x>1.
点评 本题考查了反比例函数图象上点的坐标特征、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)利用待定系数法求函数解析式;(2)利用分割图形法求三角形面积;(3)根据两函数图象的上下位置关系解不等式.本题属于中档题,难度不大,解决该题型题目时,找出点的坐标,利用待定系数法求出函数解析式是关键.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
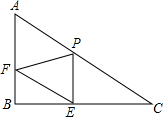 已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -a表示负数 | |
| B. | 多项式-3a2b+7a2b2-2ab+1是四次四项式 | |
| C. | 单项式-$\frac{2x{y}^{2}}{9}$的系数为-2 | |
| D. | 若|x|=-x,则x<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com