
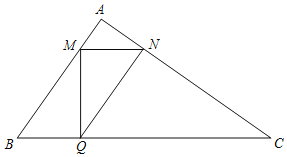
【题目】如图,在△ABC中,∠A=90°,AB=3,AC=4,点M,Q分别是边AB,BC上的动点(点M不与A,B重合),且MQ⊥BC,过点M作BC的平行线MN,交AC于点N,连接NQ,设BQ为x.
(1)试说明不论x为何值时,总有△QBM∽△ABC;
(2)是否存在一点Q,使得四边形BMNQ为平行四边形,试说明理由;
(3)当x为何值时,四边形BMNQ的面积最大,并求出最大值.
【答案】(1)证明见解析;(2)当BQ=MN时,四边形BMNQ为平行四边形,证明见解析;(3)当x=![]() 时,四边形BMNQ的面积最大,最大值为
时,四边形BMNQ的面积最大,最大值为![]() .
.
【解析】
(1)根据题意得到∠MQB=∠CAB,根据相似三角形的判定定理证明;
(2)根据对边平行且相等的四边形是平行四边形解答;
(3)根据勾股定理求出BC,根据相似三角形的性质用x表示出QM、BM,根据梯形面积公式列出二次函数解析式,根据二次函数性质计算即可.
(1)∵MQ⊥BC,
∴∠MQB=90°,
∴∠MQB=∠CAB,又∠QBM=∠ABC,
∴△QBM∽△ABC;
(2)当BQ=MN时,四边形BMNQ为平行四边形,
设AM=3a,则MN=5a,
∴BQ=MN=5a,
∵MN∥BQ,
∴∠NMQ=∠MQB=90°,
∴∠AMN+∠BMQ=90°,又∠B+∠BMQ=90°,
∴∠B=∠AMN,又∠MQB=∠A=90°,
∴△MBQ∽△NMA,
∴![]() ,即
,即![]() ,
,
解得,a=![]() ,
,
∴BQ=![]() ,
,
∵MN∥BQ,BQ=MN=![]() ,
,
∴四边形BMNQ为平行四边形;
(3)∵∠A=90°,AB=3,AC=4,
∴BC=![]() =5,
=5,
∵△QBM∽△ABC,
∴![]() ,即
,即![]() ,
,
解得,QM=![]() x,BM=
x,BM=![]() x,
x,
∵MN∥BC,
∴![]() ,即
,即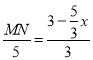 ,
,
解得,MN=5-![]() x,
x,
则四边形BMNQ的面积= ![]()
=![]() ,
,
∴当x=![]() 时,四边形BMNQ的面积最大,最大值为
时,四边形BMNQ的面积最大,最大值为![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与 y 轴交于点 C(0,4),与 x 轴交于点 A、B,点 A 的坐标为(4,0).
与 y 轴交于点 C(0,4),与 x 轴交于点 A、B,点 A 的坐标为(4,0).
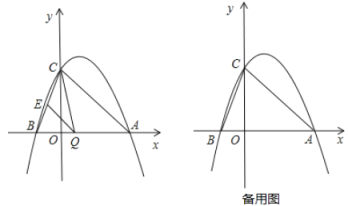
(1)求此抛物线的解析式;
(2)点 Q 是线段 AB 上的动点,过点 Q 作 QE∥AC,交 BC 于点 E,连接 CQ,当△CQE 的面积最大时,求点 Q的坐标;
(3)当点 Q 从点 B 出发沿着 BA 方向以每秒 2 个单位长向点 A 运动,同时点 P 从点 A 出发沿着 AC 方向以每秒 ![]() 个单位长度向点 C 运动,其中一个点到达终点,另一个点也停止运动,设 P、Q 运动时间为 t 秒,当 t 为何值?△APQ为等腰三角形?
个单位长度向点 C 运动,其中一个点到达终点,另一个点也停止运动,设 P、Q 运动时间为 t 秒,当 t 为何值?△APQ为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°.BE平分∠ABC交AC于点D,交△ABC的外接圆于点E,过点E作EF⊥BC交BC的延长线于点F.请补全图形后完成下面的问题:
(1)求证:EF是△ABC外接圆的切线;
(2)若BC=5,sin∠ABC=![]() ,求EF的长.
,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交点C,抛物线
与x轴交于点A,与y轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
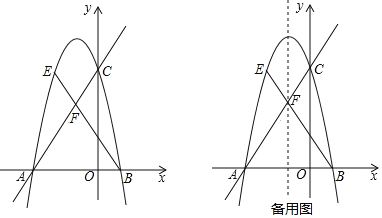
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求
时,求![]() 的值.
的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宣和中学图书馆今日购进甲、乙两种图书,每本甲种图书的进价比每本乙种图书的进价高20元,花780元购进甲种图书的数量与花540元购进乙种图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元;
(2)宣和中学购进甲、乙两种图书共70本,总购书费用不超过3950元,则最多购进甲种图书多少本.
查看答案和解析>>
科目:初中数学 来源: 题型:
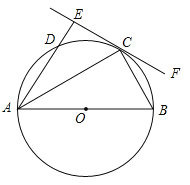
【题目】如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧![]() 的长l.
的长l.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展为贫困山区孩子捐书活动,要求捐赠的书籍类别为科普类、文学类、漫画类、哲学故事类、环保类,学校图书管理员对所捐赠的书籍随机抽查了部分进行统计,并对获取的数据进行了整理,根据整理结果,绘制了如图所示的两幅不完整的统计图.已知所统计的数据中,捐赠的哲学故事类书籍和文学类书籍的数量相同.请根据以上信息,解答下列问题:
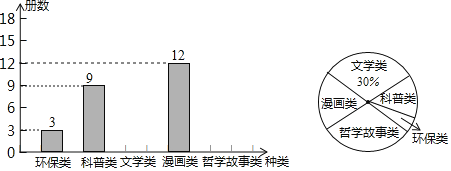
(1)本次被抽查的书籍有_____册.
(2)补全条形统计图.
(3)若此次捐赠的书籍共1200册,请你估计所捐赠的科普类书籍有多少册.
查看答案和解析>>
科目:初中数学 来源: 题型:
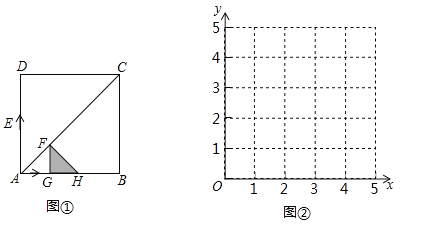
【题目】如图①,正方形ABCD的边长为4,动点E从点A出发,以每秒2个单位的速度沿A﹣D﹣A连续做往返运动;动点G从点A出发,以每秒1个单位的速度沿AB方向运动.E、G两点同时出发,当点G到达点B时停止运动,点E也随之停止.过点G作FG⊥AB交AC于点F,以FG为一直角边向右作等腰直角三角形FGH,使∠FGH=90°.设点G的运动时间为t(秒),△FGH与正方形ABCD重叠部分图形的周长为l.
(1)当t=1时,l= .
(2)当t=3时,求l的值.
(3)设DE=y,在图②的坐标系中,画出y与t的函数图象.
(4)当四边形DEGF是平行四边形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查。将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
(1)通过计算补全条形统计图;
(2)在这次调查中,一共抽取了多少名学生?
(3)如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?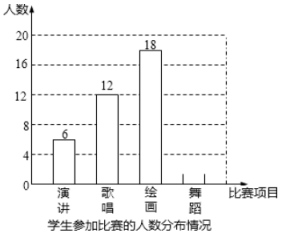
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com