
分析 (1)设甲型计算器进价是x元,乙型计算器进价是y元,根据购进甲型计算器3只和乙型计算器5只,共需要资金370元;若购进甲型计算器2只和乙型计算器7只,共需要资金430元即可列方程组求解;
(2)设购进甲型计算器为a只,则购进乙型计算器为(50-a)只,根据用于购买这两种型号的计算器的资金不少于2250元但又不超过2270元即可列不等式组求得a的范围,然后根据a是正整数从而求得a的值;
(3)根据(2)中a的值确定方案,求得获利,即可进行比较.
解答 解:(1)设甲型计算器进价是x元,乙型计算器进价是y元
得:$\left\{\begin{array}{l}3x+5y=270\\ 2x+7y=430\end{array}\right.$,解得:$\left\{\begin{array}{l}x=40\\ y=50\end{array}\right.$.
每只甲型计算器进价是40元,每只乙型计算器进价是50元.
(2)设购进甲型计算器为a只,则购进乙型计算器为(50-a)只,
得:$\left\{\begin{array}{l}40a+50(50-a)≤2270\\ 8a+12(50-a)≥500\end{array}\right.$
解得:23≤a≤25,
因为a是正整数,所以a=23,24,25.
该经销商有3种进货方案:
①方案一:购进23只甲型计算器,27只乙型计算器;
②方案二:购进24只甲型计算器,26只乙型计算器;
③方案三:购进25只甲型计算器,25只乙型计算器.
(3)方案一商家可获利(432-4m)元;
方案二商家可获利(416-2m)元;
方案三商家可获利400元.
当m=8时,三种方案获利相同
当0≤m<8时,方案一获利最多
当8<m≤16时,方案三获利最多
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.


科目:初中数学 来源: 题型:解答题
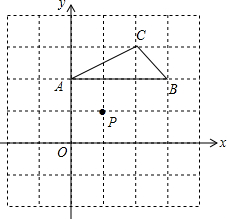 如图,在平面直角坐标系中,点A,B,C,P的坐标分别为(0,2),(3,2),(2,3),(1,1).
如图,在平面直角坐标系中,点A,B,C,P的坐标分别为(0,2),(3,2),(2,3),(1,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,请你猜想图中哪两条线段之和等于第三条线段,并证明你的猜想的正确性(证明你的猜想需要用题中所有的条件).
如图,在△ABC中,∠A=90°,AB=AC,BD是∠ABC的平分线,请你猜想图中哪两条线段之和等于第三条线段,并证明你的猜想的正确性(证明你的猜想需要用题中所有的条件).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
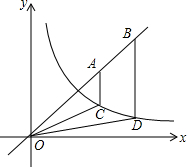 如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线$y=\frac{1}{x}$(x>0)于C,D两点.若BD=2AC.
如图,点A,B为直线y=x上的两点,过A,B两点分别作y轴的平行线交双曲线$y=\frac{1}{x}$(x>0)于C,D两点.若BD=2AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{91}{216}$ | B. | $\frac{31}{216}$ | C. | $\frac{13}{216}$ | D. | $\frac{19}{216}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<-1 | B. | a<1 | C. | a>-1 | D. | a>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com