
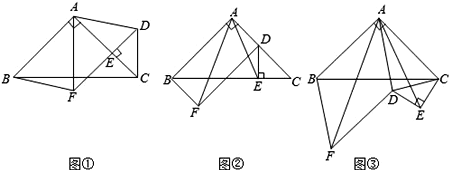
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论.
![]()
【答案】(1)AF=![]() AE;
AE;
(2)AF=![]() AE,证明见解析.
AE,证明见解析.
【解析】解:(1)如图①中,∵四边形ABFD是平行四边形,
∴AB=DF,∵AB=AC,∴AC=DF,∵DE=EC,∴AE=EF,
∵∠DEC=∠AEF=90°,∴△AEF是等腰直角三角形, ∴AF=![]() AE.
AE.
(2)如图②中,连接EF,DF交BC于K.
∵四边形ABFD是平行四边形,∴AB∥DF,
∴∠DKE=∠ABC=45°,∴EKF=180°﹣∠DKE=135°,
∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,∴∠EKF=∠ADE,
∵∠DKC=∠C,∴DK=DC,∵DF=AB=AC,∴KF=AD, 在△EKF和△EDA中,
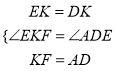 ,
,
∴△EKF≌△EDA, ∴EF=EA,∠KEF=∠AED,
∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,∴AF=![]() AE.
AE.


科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投出多少个3分球?共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A,B,C三点; 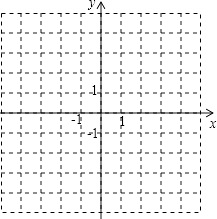
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在![]() 的方格(每小格边长为
的方格(每小格边长为![]() )上沿着网格线运动,网格线与网格线的交点为格点,甲虫从
)上沿着网格线运动,网格线与网格线的交点为格点,甲虫从![]() 处出发去看望格点
处出发去看望格点![]() 、
、![]() 、
、![]() 处的其它甲虫,若规定:向上向右走均为正,向下向左走均为负,如果从
处的其它甲虫,若规定:向上向右走均为正,向下向左走均为负,如果从![]() 到
到![]() 记为:
记为:![]() ,从
,从![]() 到
到![]() 记为:
记为:![]() ,其中第一个数表示左右方向,第二个数表示上下方向.
,其中第一个数表示左右方向,第二个数表示上下方向.
(![]() )图中
)图中![]() __________.
__________.
(![]() )若这只甲虫从
)若这只甲虫从![]() 处出发,行走路线依次为
处出发,行走路线依次为![]() ,
,![]() ,
,![]() ,
,![]() ,最后在
,最后在![]() 点停止运动,请在图中标出点
点停止运动,请在图中标出点![]() 的位置.
的位置.
(![]() )若这只甲虫的行走路线为
)若这只甲虫的行走路线为![]() ,则该甲虫走过的路程长度为__________.
,则该甲虫走过的路程长度为__________.
(![]() )若图中另有两个格点
)若图中另有两个格点![]() 、
、![]() ,且
,且![]() ,
,![]() ,则
,则![]() 应记为__________.
应记为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年6月18日为父亲节,某校准备开展形式多样的感恩教育活动.下面图①、图②分别是该校调查部分学生是否知道父亲生日情况的扇形统计图和频数分布直方图.
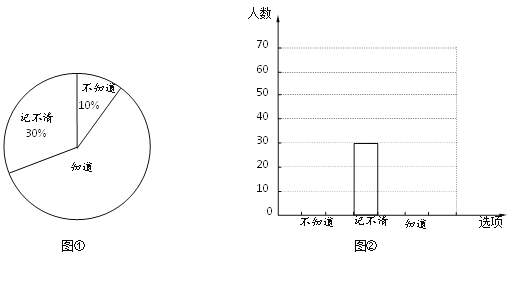
根据上图信息,解答下列问题:
(1)本次被调查的学生总数有 人,并补全频数分布直方图②;
(2)在扇形统计图中,学生知道父亲生日的区域圆心角为 o;
(3)若这所学校共有学生1500人,请你估计该校知道父亲生日的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
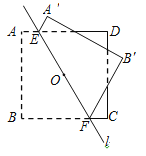
【题目】如图,正方形ABCD的边长为2,点O是正方形的中心,过点O作一条直线l分别交正方形AD,BC两边于点E,F.直线l将正方形分成两部分,将其中的一个部分沿这条直线翻折到另一个部分上,若AE=![]() ,则两个部分图形中不重叠部分的面积为_______.
,则两个部分图形中不重叠部分的面积为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com