
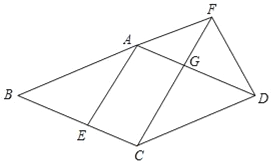
【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G.
求证:(1)FD=CG;
(2)CG2=FGFC.
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)先由菱形性质得∠FAD=∠B,再由全等三角形的判定定理得△ADF≌△BAE,进而得到FD=EA,由两组对边分别平行的四边形是平行四边形得到结论;(2)由两直线平行内错角相等得到∠DCF=∠BFC,由两直线平行同位角相等得到∠BAE=∠BFC,进而∠DCF=∠BAE,由全等三角形对应角相等得到∠BAE=∠FDA,∠DCF=∠FDA,再由相似三角形的判定得到△FDG∽△FCD,由相似性质得到结论.
试题解析:证明:(1)∵在菱形ABCD中,AD//BC,∴∠FAD=∠B,
又∵AF=BE,AD=BA,∴△ADF≌△BAE.
∴FD=EA,
∵CF//AE,AG//CE,∴EA=CG.
∴FD=CG.
(2)∵在菱形ABCD中,CD//AB,∴∠DCF=∠BFC.
∵CF//AE,∴∠BAE=∠BFC,∴∠DCF=∠BAE.
∵△ADF≌△BAE,∴∠BAE=∠FDA,∴∠DCF=∠FDA.
又∵∠DFG=∠CFD,∴△FDG∽△FCD.
∴![]() ,
, ![]() .
.
∵FD=CG, ![]() .
.


科目:初中数学 来源: 题型:
【题目】坐标平面上有一点A,且A点到x轴的距离为3,A点到y轴的距离恰为到x轴距离的3倍,若A点在第二象限,则A点坐标为( )
A. (﹣3,9)B. (﹣3,1)C. (﹣9,3)D. (﹣1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
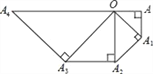
【题目】如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA6的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明要从长度分别为5cm,6cm,11cm,16cm的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒形成的三角形的周长为( )cm
A.22B.27C.33D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句:
①对顶角相等
②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直;
③过一点有且只有一条直线与已知直线平行,其中( )
A.①、②是正确的命题B.②、③是正确命题
C.①、③是正确命题D.以上结论皆错
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两种包装盒,大盒比小盒可多装20克某一物品.已知120克这一物品单独装满小盒比单独装满大盒多1盒.
(1)问小盒每个可装这一物品多少克?
(2)现有装满这一物品两种盒子共50个.设小盒有n个,所有盒子所装物品的总量为w克.
①求w关于n的函数解析式,并写出定义域;
②如果小盒所装物品总量与大盒所装物品总量相同,求所有盒子所装物品的总量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.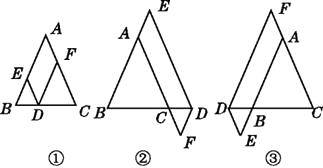
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③.请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com