
【题目】如图,在Rt△ABC中,∠C=90°,BD是△ABC的一条角平分线.点O、E、F分别在BD、BC、AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
【答案】
(1)证明:过点O作OM⊥AB, 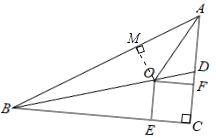
∵BD是∠ABC的一条角平分线,
∴OE=OM,
∵四边形OECF是正方形,
∴OE=OF,
∴OF=OM,
∴AO是∠BAC的角平分线,即点O在∠BAC的平分线上
(2)解:∵在Rt△ABC中,AC=5,BC=12,
∴AB= ![]() =
= ![]() =13,
=13,
设CE=CF=x,BE=BM=y,AM=AF=z,
∴ 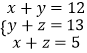 ,
,
解得: 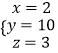 ,
,
∴CE=2,
∴OE=2.
【解析】(1)过点O作OM⊥AB,根据角平分线的性质定理得出OE=OM,再根据正方形的性质得出OE=OF,从而得出OF=OM,,根据角平分线的判定定理得出结论;
(2)在Rt△ABC中,利用勾股定理得出AB的长,设CE=CF=x,BE=BM=y,AM=AF=z,根据切线长定理得出方程组,求解即可。
【考点精析】关于本题考查的切线长定理和角的平分线判定,需要了解从圆外一点引圆的两条切线,它们的切线长相等圆心和这一点的连线平分两条切线的夹角;可以证明三角形内存在一个点,它到三角形的三边的距离相等这个点就是三角形的三条角平分线的交点(交于一点)才能得出正确答案.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一个点从A(a1 , a2)出发沿图中路线依次经过B(a3 , a4),C(a5 , a6),D(a7 , a8),…,按此一直运动下去,则a2015+a2016的值为 . 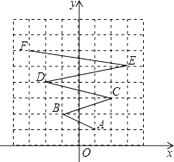
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国倡导的“一带一路”建设将促进我国与世界各国的互利合作,“一带一路”地区覆盖总人口约为4400000000人,将数据4400000000用科学记数法表示为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节前夕,某商店根据市场调查,用2000元购进第一批盒装花,上市后很快售完,接着又用4200元购进第二批这种盒装花.已知第二批所购的盒数是第一批所购花盒数的3倍,且每盒花的进价比第一批的进价少6元.求第一批盒装花每盒的进价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以A(0, ![]() )为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
)为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
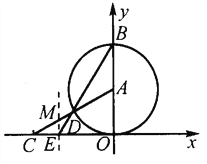
(1)分别求点E、C的坐标;
(2)求经过A、C两点,且以过E而平行于y轴的直线为对称轴的抛物线的函数解析式;
(3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心,ME为半径的圆与⊙A的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式由左到右的变形中,属于因式分解的是( )
A. a(m+n)= am+an B. a2﹣b2﹣c2 =(a﹣b)(a+b)﹣c2
C. 10x2﹣5x = 5x(2x﹣1) D. x2﹣16+6x =(x+4)(x﹣4)+ 6x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中任意一点p(x,y)经平移后对应点为p1(x+5,y+3),将△ABC作同样的平移得到△A1B1C1.
(1)画出△A1B1C1;
(2)求A1,B1,C1的坐标;
(3)写出平移的过程.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com