
【题目】某种子培育基地用A,B,C,D四种型号的小麦种子共2 000粒进行发芽实验,从中选出发芽率高的种子进行推广.通过实验得知,C型号种子的发芽率为95﹪,根据实验数据绘制了图-1和图-2两幅尚不完整的统计图.
(1)D型号种子的粒数是______;
(2)请你将图-2的统计图补充完整;
(3)通过计算说明,应选哪一个型号的种子进行推广;
(4)若将所有已发芽的种子放到一起,从中随机取出一粒,求取到B型号发芽种子的概率

【答案】解:(1)D型号种子的粒数为2000×(1-35%-20%-20%)=500(粒),C型号种子的发芽数为:2000×20%×95%=380(粒),画图略.………3分
(2)A种型号种子的发芽率为:630÷(2000×35%)=90%;
B种型号种子的发芽率为:370÷(2000×20%)=92.5%;
D种型号种子的发芽率为:470÷500=94%,又已知C种型号种子的发芽率为95%,
所以,C型号种子的发芽率最高,故应选择C型号种子进行推广. ………7分
(3)四种型号种子的总发芽数为:630+370+470+380=1850(粒),B种子的发芽数为370粒,
所以取到B型号种子的概率为:P=![]() .…………………………9分
.…………………………9分
【解析】略


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形…依次进行下去,则第n个内接正方形的边长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出一种运算:对于函数y=xn,规定y'=n×xn﹣1.若函数y=x4,则有y'=4×x3,已知函数y=x3,则方程y'=6x的解是( )
A. x=2B. x=3C. x1=0,x2=2D. x=﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)甲乙两地之间的距离为______千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】振子从一点A开始左右来回振动8次,如果规定向右为正,向左为负,这8次振动记录为(单位:毫米):+10,﹣9,+8,﹣6,+7.5,﹣6,+8,﹣7.
(1)求振子停止时所在位置距A点有多远?
(2)如果每毫米需时间0.02秒,则共用时间多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是一块等边三角形场地,点D,E分别是AC,BC边上靠近C点的三等分点.现有一个机器人(点P)从A点出发沿AB边运动,观察员选择了一个固定的位置记录机器人的运动情况.设AP=x,观察员与机器人之间的距离为y,若表示y与x的函数关系的图象大致如图2所示,则观察员所处的位置可能是图1的( )

A. 点B B. 点C C. 点D D. 点E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 有一组对角是直角的四边形一定是矩形 B. 有一组邻角是直角的四边形一定是矩形
C. 对角线互相平分的四边形是矩形 D. 对角互补的平行四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.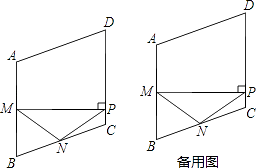
(1)若∠B=60°,这时点P与点C重合,则∠NMP=度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com