
分析 如图,AB=AC,BD是△ABC的角平分线,BE是高,BD=2BE,AF⊥BC于F,设∠CBE=∠CAF=∠BAF=x,则∠DBC=x-60°,列出方程即可解决问题.
解答 解:如图,AB=AC,BD是△ABC的角平分线,BE是高,BD=2BE,AF⊥BC于F,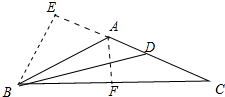
在Rt△BDE中,∵BD=2BE,
∴∠BDE=30°,∠DBE=60°,
∵∠C+∠CAF=90°,∠C+∠CBE=90°,
∴∠CBE=∠CAF=∠BAF,设∠CBE=∠CAF=∠BAF=x,则∠DBC=x-60°,
∴2x+4(x-60°)=180°,
∴x=70°,
∴∠BAC=2x=140°,
∴等腰三角形顶角的度数为140°.
点评 本题考查角平分线的性质、等腰三角形的性质、三角形内角和定理等知识,解题的关键是灵活应用知识知识解决问题,属于中考常考题型.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
 美是一种感觉,当人的肚脐是人的身高的黄金分割点时,如图人的下半身长m与身高l之比约为0.618,人的身段成为黄金比例,给人一种美感.某女士身高165cm,下半身长与身高的比值是0.60,为尽可能达到匀称的效果,她应穿高跟鞋的高度大约为8cm.(结果保留整数)
美是一种感觉,当人的肚脐是人的身高的黄金分割点时,如图人的下半身长m与身高l之比约为0.618,人的身段成为黄金比例,给人一种美感.某女士身高165cm,下半身长与身高的比值是0.60,为尽可能达到匀称的效果,她应穿高跟鞋的高度大约为8cm.(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com